Migration-Contagion Processes
Consider a migration process based on a closed network of N stations with KN customers. Each station is a ./M/\infty queue with service (migration) rate mu. Upon departure, a customer is routed at random to another station. In addition to migration, these customers are subject to an SIS (Susceptible, Infected, Susceptible) dynamics: customers are either I for infected, or S for susceptible. They can swap their state either from I to S or from S to I only in stations. At any station, each S customer becomes I with rate alpha Y if there are Y infected customers in the station, and each I customer recovers and becomes S with rate beta. We let N tend to infinity and assume that lim_{N\to infty} K_N/N= eta>0. The main problem is about the set of parameters for which there exists a stationary regime where the epidemic survives in the thermodynamic limit. We establish several structural properties of the system, which allow us to give the phase transition diagram of this thermodynamic limit w.r.t. eta. The analysis of the SIS model reduces to that of a wave-type PDE for which we found no explicit solution. This SIS model is one among several companion stochastic processes with migration and contagion. Two of them are discussed as they provide some bounds and approximations to SIS. These two variants are the DOCS (Departure On Change of State) and the AIR (Averaged Infection Rate), which both admit closed-form solutions. The AIR system is a mean-field model where the infection mechanism is based on the empirical average of the number of infected customers in all stations. The latter admits a product-form solution. DOCS features accelerated migration in that each change of SIS state implies an immediate departure. It leads to another wave-type PDE that admits a closed-form solution.
- F. Baccelli, S. Foss, and S. Shneer, ‘Migration Contagion Processes’, Advances in Applied Probability, 2023. Paper .
A Computational Framework for Evaluating the Role of Mobility on the Propagation of Epidemics on Point Processes
This paper in collaboration with Nithin Ramesan (UT Austin, Electrical and Computer Engineering), is focused on SIS epidemic dynamics (also known as the contact process) on stationary Poisson point processes of the Euclidean plane, when the infection rate of a susceptible point is proportional to the number of infected points in a ball around it.
Two models are discussed, the first with a static point process, and the second where points are subject to some random motion.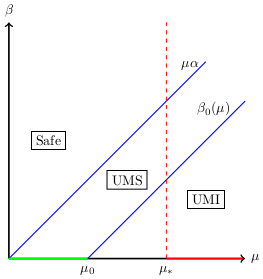
For both models, we use conservation equations for moment measures to analyze the stationary point processes of infected and susceptible points.
A heuristic factorization of the third moment measure is then proposed to derive simple polynomial equations allowing one to derive closed form approximations for the fraction of infected nodes and the steady state.
These polynomial equations also lead to a phase diagram which tentatively delineates the regions of the space of parameters (population density, infection radius, infection and recovery rate, and motion rate) where the epidemic survives and those where there is extinction. According to this phase diagram, the survival of the epidemic is not always an increasing function of the motion rate.
These results are substantiated by simulations on large two dimensional tori. These simulations show that the polynomial equations accurately predict the fraction of infected nodes when the epidemic survives.
The phase diagram is also partly substantiated by the simulation of the mean survival time of the epidemic on large tori. The phase diagram accurately predicts the parameter regions where the mean survival time increases or decreases with the motion rate.
For more on the matter, see
- F. Baccelli, and N. Ramesan, ‘A computational framework for evaluating the role of mobility on thew
propagation of epidemics on point processes’, Journal of Mathematical Biology, volume 84, (January 2022). DOI : 10.1007/s00285-021-01692-1, URL : https://hal.science/hal-03542621
Galves-Löcherbach Dynamics
For the line of thoughts on the Galves-Löcherbach type dynamics for neural networks, see the Mean-Field Limit page.
