Télécharger la documentation en pdf: Click here.
Présentation
Présentation
Cette section contient une présentation du logiciel, de son but et de son fonctionnement ainsi que la présentation et la description des modèles présent dans le logiciel et pouvant être simulés.
FiatLux
FiatLux est un simulateur d’automates cellulaires dans des espaces en une ou deux dimensions finis. Il permet la création de modèles déterministes ou stochastiques et la visualisation de l’évolution des systèmes. Spécialement conçu pour l’étude de la robustesse des modèles il permet le découplage des éléments des modèles permettant de changer de fonction de mise à jour, l’étendue de l’espace, le choix du voisinage et d’autres propriétés. Le logiciel propose plusieurs fonctionnalités permettant l’étude des modèles avec des outils d’analyses tels que la densité de cellules dans un état donné ou le taux de variation de cellules. Ses caractéristiques distinctives sont de permettre de perturber la mise à jour du système avec un taux de synchronisation paramétrable et d’agir sur la topologie du réseau.
Cas d’utilisations
Simulation d’un automate cellulaire à une dimension
Avec l’exemple de l’ECA définissant la règle 150.
Une fois le logiciel lancé le menu s’affiche. La liste des modèles présents dans l’application se trouve dans la partie 3 Modèles . Néanmoins, la plupart des automates cellulaires à une dimension se trouvent dans l’onglet « linear ». Après avoir cliqué sur l’onglet linear l’utilisateur doit sélectionner le modèle qu’il vaut lancer (ici ECA).
Le bon voisinage dans la section « Neighborhood » pour les ECA est sélectionné de base (LineR-1) mais l’utilisateur peut en sélectionner un autre suivant le modèle qu’il choisit de lancer1.
L’utilisateur doit ensuite régler la taille de la grille2. Pour cela il doit se servir des boutons + / – servent à multiplier ou diviser le nombre de cellule de l’espace par deux. L’utilisateur peut aussi rentrer la valeur qu’il souhaite dans le paramètre « N Cells » qui affichent le nombre de cellules présentes dans l’espace ou bien sélectionner l’un des presets disponibles (initialement « medium » est choisi).
L’utilisateur peut aussi adapter le «time buffer» afin de voir plus d’état passés de la simulation.
L’utilisateur choisit ensuite le type d’espace qu’il veut pour sa simulation. Le mode par défaut (Toric)3 est celui conseillé. Si besoins l’utilisateur peut choisir de prendre la condition au bord de la simulation «inert» avec un certain taux d’apparitions et de mise à jour.
Une fois tous ces réglages faits l’utilisateur doit cliquer sur « Open » de la table de contrôle4 afin de lancer le simulateur. Une nouvelle fenêtre s’ouvre5.
Dans le cas des ECA (et d’autres modèles) des paramètres s’affichent en haut du simulateur dans la zone grisée. Le seul paramètre du modèle choisit dans cet exemple est « ECA »6 c’est dans cet encadré que l’utilisateur doit rentrer la règles voulue (ici 150).
Dans le simulateur la table de contrôle permet de lancer, de mettre en pause et de faire avancer la simulation7. La partie «Initializer» permet d’effacer toutes les cellules grâce au bouton «clear» et de définir comment les cellules seront générés lors d’une initialisation8. Enfin la plupart des modèles permettent aussi de décider « à la main » comment initialiser les cellules. Pour cela il suffit de cliquer sur une cellule de la dernière itération (l’espace tout en haut du Viewer dans la configuration initiale du logiciel) pour changer son état.
Simulation d’un automates cellulaire à deux dimensions
Avec l’exemple du «jeu de la vie».
Une fois le logiciel lancé le menu s’affiche. La liste des modèles présents dans l’application se trouve dans la partie 3 Modèles . Les automates cellulaires à deux dimensions les plus connus se trouvent dans l’onglet « general » ouvert initialement dans l’application. L’utilisateur peut sélectionner le modèle qu’il vaut lancer (ici Life).
Le bon voisinage dans la section « Neighborhood » pour les ECA est sélectionné de base (Moore8) mais l’utilisateur peut en sélectionner un autre suivant le modèle qu’il choisit de lancer9.
L’utilisateur doit ensuite adapter la taille de la grille10. Pour cela il doit sélectionner l’un des presets disponibles (initialement « medium » est choisi). Les boutons + / – servent à multiplier ou diviser le nombre de cellule de l’espace par deux. L’utilisateur peut aussi rentrer la valeur qu’il souhaite pour la taille de la grille en X et en Y avec le paramètre « Size ».
L’utilisateur choisit ensuite le type d’espace qu’il veut pour sa simulation. Le mode par défaut (Toric)11 est celui conseillé. Si besoins l’utilisateur peut choisir de prendre la condition au bord de la simulation «inert» avec un certain taux d’apparitions et de mise à jour.
Une fois tous ces réglages faits l’utilisateur doit cliquer sur « Open » de la table de contrôle12 afin de lancer le simulateur. Une nouvelle fenêtre s’ouvre13.
Dans le simulateur la table de contrôle permet de lancer, de mettre en pause et de faire avancer la simulation14. La partie «Initializer» permet d’effacer toutes les cellules grâce au bouton «clear» et de définir comment les cellules seront générés lors d’une initialisation15. Enfin la plupart des modèles permettent aussi de décider « à la main » comment initialiser les cellules. Pour cela il suffit de cliquer sur une cellule pour changer son état.
Notation d’automates cellulaires
Plusieurs modèles nécessitent que l’utilisateur rentre une valeur pour lancer le modèle demandé. Ici sont décris les deux notations possible de règle d’automates cellulaires. La notation dite de Wolfram utilisant des valeurs binaires et la notation de transition utilisant les lettres.
Notation de Wolfram
Pour un automate à une condition
Puisque il n’y a que les deux plus proches voisins et l’état de la cellule pris en compte et qu’il n’y a que deux états possible il n’y a donc que 8 possibilités de voisinage (voir le tableau plus bas : l’état de la cellule est le chiffre du milieu et les deux chiffres autours représentent l’état des cellules voisines). En fonction du résultat de la mise à jour de la cellule (0 ou 1) il y a donc 28 (soit 256) fonction de mise à jour possible. Il est possible d’utiliser cela pour donner une valeur à partir de données binaires et c’est comme cela que sont nommés les fonctions de mise à jour des ECAs Rule + valeur binaire.
| État du voisinage | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
|---|---|---|---|---|---|---|---|---|
| Valeur binaire | 20 = 1 | 21 = 2 | 22 = 4 | 23 = 8 | 24 = 16 | 25 = 32 | 26 = 64 | 27 = 128 |
Un exemple d’utilisation du tableau ci-dessus est la «150» aussi appelée «XoR3». Avec les valeurs binaires pour chaque état possible du voisinage il n’y a qu’un seul moyen d’obtenir le nombre 150. C’est en faisant 128 (de l’état 111) + 16 (de l’état 100) + 4 (de l’état 010) + 2 (de l’état 001). Cela signifie que seuls les quatre états cités précédemment donneront une cellule à l’état 1 lors de la prochaine mise à jour du système. Les autres états du voisinage renverront a l’état 0.
Cela veut donc dire que la règle de mise à jour «Rule 150» est : si la cellule est à l’état 1 et que ses deux voisins sont à l’état 1 ou 0 elle sera à l’état 1 a la prochaine mise à jour. Si la cellule est à l’état 0 mais que l’un de ses voisins est à l’état 1 alors elle sera à l’état 1 lors de la prochaine mise à jour. Dans les autres cas la cellule sera à l’état 0.
Pour un automate à deux condition
Pour définir la table de transition d’une règle il est possible de cocher les états où la cellule est vivante en fonction du nombre de voisins vivants. Il est aussi possible de rentrer une valeur ce qui peut être plus simple pour la compréhension : Pour cela il y a pour chaque nombre de voisins vivants une valeur binaire qui lui est donnée (voir le tableau plus bas). La notation d’une règle est donc l’addition des valeurs binaires du nombre de voisins vivants nécessaires pour que la cellule soit vivante.
s
Par exemple la règle du jeu de la vie est passage de 0 à 1 si la cellule possède trois voisins vivants et reste vivant si possède 2 ou 3 voisins vivant. La valeur de cette règle est donc: 26 + 25 + 27 = 224.
Notation de transition
Cette notation (inventée par le créateur de FiatLux) n’est pas couramment utilisée et seul ce logiciel la prend en compte à notre connaissance. Elle permet néanmoins une écriture plus courte dans certains cas et surtout une meilleure visualisation de la fonction de mise à jour qu’un simple nombre.
Ici sont repris les 8 états du voisinage possible comme décris plus haut mais ils sont triés dans un autre ordre : Nous avons d’abord les cas où la cellule principale est à l’état 0 puis ceux ou la cellule est à l’état 1. A chacun de ses voisinages possibles est associé une lettre. Et pour nommer une règle de mise à jour il faut prendre les lettres où l’état par défaut de la cellule va changer.
| État du voisinage | 000 | 001 | 100 | 101 | 010 | 011 | 110 | 111 |
|---|---|---|---|---|---|---|---|---|
| Valeur alphabétique | A | B | C | D | E | F | G | H |
Comme exemple nous allons faire passer la «Rule XOR3» de la notation binaire vers la notation de transitions: La valeur binaire de la règle est 150 car les cas qui donnent une cellule à l’état 1 sont les voisinages 111, 100, 010 et 001. Avec la notation de transition on ne prend pas les lettres des voisinages donnant 1 mais des voisinages qui feront que la cellule principale va changer d’états : les cas qui vont donner des transitions. Ici le cas 111 donne une cellule à l’état 1, il n’y a pas eut de transitions donc on ne note pas cette lettre. Il en va de même pour le voisinage 010. Par contre, le voisinage 100 et 001 font transiter l’état de la cellule. On note donc les lettres B et C. Ensuite, il y a les cas ou la cellule est déjà à l’état 1 mais où elle va passer à l’état 0. Ce sont les cas 011 et 110 pour XOR3. On note donc aussi les lettres F et G. Nous y voila, «Rule XOR3» peut donc s’écrire «Rule 150» et «Rule BCFG» et c’est une de ces deux valeurs qu’il faudra rentrer dans le logiciel.
Modèles présents initialement
Les modèles présents sont présentés dans différentes sections. Il y a, dans l’ordre de classement, les automates cellulaires tel que l’entend la définition classique, les systèmes complexes dit de «Lattice-Gaz», les systèmes multi-agents et les systèmes complexes particulaires.
Onglet «cellular automata»
Onglet contenant les modèles d’automates cellulaires «standards». Puisque cette section contient un nombre important de modèles elle a été redivisée en plusieurs parties:
Onglet general
La sous-section «general» accueil les automates cellulaires les plus connus pouvant être simulés selon une topologie unidimensionnelle ou bidimensionnelle. [General] [Life]
Game of Life :
Automate cellulaire le plus connu, inventé par John Horton Conway et rendu célèbre par Martin Gardner. Les règles sont simples : si une cellule à l’état morte possède trois voisins à l’état vivante elle passe a l’état vivante. Si une cellule vivante possède moins de deux voisins vivants ou plus de 3 voisins vivants elle meurt. Cet automate a passé est donc capable de calculabilité universelle.
Le jeu de la vie est plus spectaculaire (et intéressant) en 2D avec le voisinage Moore816 qui est sélectionnée par défaut.
[Majority]
Majority :
Automate cellulaire à deux états où les cellules prennent l’état majoritairement présent dans leur voisinage .
[Minority]
Minority :
Automate cellulaire à deux états où les cellules prennent l’état minoritaire de leur voisinage.
[Parity]
Parity :
Automate cellulaire à deux états où les cellules prennent la valeur 0 si le nombre de cellules à l’état 1 dans leur voisinage est pair (cela comprend 0) et 1 si le nombre de voisins à 1 est impair. Cet automate possède en 2D une propriété d’auto-reproduction triviale.
[Totalistic]
Totalistic :
Les automates cellulaires totalisants sont les automates cellulaires dont la mise à jour des cellules dépend uniquement du nombre total de voisins dans l’état 1. Le paramètre «ECA» demande une valeur d’un automate cellulaire17. Mais il est aussi possible de générer cette valeur visuellement en cochant les cases du tableau dans la section «paramètres18» de l’interface: En fonction du nombre de voisins (l’entrée du tableau) l’utilisateur peut sélectionner le fait que la cellule reste ou passe à l’état vivant.
[OuterTotalistic]
OuterTotalistic :
Ce genre d’automate cellulaire contient les automates dont la mise à jour des cellules dépend de l’état initial de la cellule et du nombre de voisins à l’état 1. Le jeu de la vie est un automate cellulaire de ce type. Le paramètre «ECA» demande une valeur d’un automate cellulaire19. Mais il est aussi possible de générer cette valeur visuellement en cochant les cases du tableau dans la section «paramètres20» de l’interface: En fonction du nombre de voisins (l’entrée du tableau) l’utilisateur peut sélectionner le fait que la cellule passe à l’état vivant (première ligne du tableau) ou reste à l’état vivant (seconde ligne du tableau).
[React-Diff]
Réaction-Diffusion :
Automate cellulaire modélisant un système de réaction-diffusion. C’est un modèle décrivant l’évolution des concentrations d’un état d’excitation soumis à deux processus : le premier, celui de la Réaction est le processus d’excitation de la cellule et le second, la diffusion, est celui qui provoque la répartition de cet état dans l’espace. Le premier état (orange) représente l’état excité et les autres un état de «latence» représentant le fait que cellule ne peut plus être excitée durant un certain temps . Le meilleur exemple de ce modèle est celui de la «Ola» : Une personne commence par faire la Ola, est suivie par ses voisins, dont leurs voisins enchaînent et ainsi de suite. Puis lorsque les spectateurs se rassoient ils ne vont pas recommencer tout de suite. Une fois assis à nouveau, si leurs voisins font la Ola ils la reprendront.
[ForestFire]
Forest fire :
Est une modélisation simple des feux de forets. Chaque cellule vide peut devenir de la végétation et chaque portion de végétation peut prendre feu. Si une cellule de végétation se situe à coté d’une cellule en feu elle prend feu à son tour. Ces deux probabilités (végétation qui pousse et inflammation) sont paramétrables.
[Voronoi]
Voronoi :
Automate cellulaire implémentant de manière discrète le diagramme de Voronoï. Le diagramme de Voronoï est un pavage de plan (ici de l’espace du modèle) en régions découpées à partir de points (ici de cellules) nommées germes. Chaque région ne contient qu’un seul germe et la région d’un germe ne doit contenir que les espaces plus proches de ce germe-ci plutôt que d’un autre. Dans cette implémentation en automate cellulaire chaque germe contient un état. Chaque cellule vide prend l’état des voisins si ceux-ci possèdent un état. S’il y a confrontation entre deux états la cellule prend un état unique.
Onglet linear
Les automates cellulaires linéaires regroupent les modèles les plus connus en une dimension.
[Linear] [ECA]
Elementary Cellular Automaton (ECA) :
Les ECA sont des automates cellulaires à une dimension et deux états (0 ou 1) et généralement étudiés ensemble. Les ECAs sont particulièrement bien connus: l’espace est en une dimension et le voisinage des cellules contient les 2 cellules immédiatement voisines droite et gauche (dans FiatLux il est possible de changer le voisinage des ECAs mais il faut bien comprendre que cela n’a aucun sens au niveau mathématique). En fonction de l’état de ses voisins et de son propre état chaque cellule va se mettre à jour suivant la règle choisie. Le paramètre «ECA» demande une valeur d’un automate cellulaire21.
[FuzzyECAalgebraic]
Fuzzy ECA Algebrique :
Les modélisations dites «Fuzzy» ont le même fonctionnement que les modélisations dont elles portent le nom (ici les ECAs22) à ceci près que les valeurs des cellules n’est pas binaire (ou absolue si le modèle comporte plusieurs états, ce qui n’est de toute manière pas le cas ici). Les valeurs des cellules sont des nombres réels et non plus des entiers comme c’est le cas des modèles «non-Fuzzy». La fonction de mise à jour est donc un calcul algébrique reprenant la valeur des états des voisins pour calculer le futur état de sa cellule. Donc plutôt que d’avoir des cellules à l’état 0 ou 1 il va y avoir une infinité d’états possibles entre 0 et 1 (incluant ces deux derniers).
[FuzzyDiploidECA]
Fuzzy Diploïd ECA :
Les modélisations dites «Fuzzy» ont le même fonctionnement que les modélisations dont elles portent le nom (ici les ECAs Dilpoïd23) à ceci près que les valeurs des cellules n’est pas binaire (ou absolue si le modèle comporte plusieurs états, ce qui n’est de toute manière pas le cas ici). Les valeurs des cellules sont des nombres réels et non plus des entiers comme c’est le cas des modèles «non-Fuzzy». La fonction de mise à jour est donc un calcul algébrique reprenant la valeur des états des voisins pour calculer le futur état de sa cellule. Donc plutôt que d’avoir des cellules à l’état 0 ou 1 il va y avoir une infinité d’états possibles entre 0 et 1 (incluant ces deux derniers).
Onglet particles
[Particles]
Les automates cellulaires dont les fonctions de mise à jour cellules sont moins au centre de la modélisation plutôt que des entités, nommées «agents», qui ont des propriétés et des fonctionnements propres. L’espace reste divisé en cellules mais dans cet espace interagissent les agents prenant place dans les cellules comme des pions sur une case d’un jeu d’échec. Ces automates cellulaires sont regroupés sous le terme «Particule» car ce sont les interactions entre ces particules identiques (les agents) qu’il est intéressant d’observer.
[Dictyo]
Dictyo:
Ce modèle a été mis en place afin de résoudre le problème du «regroupement décentralisé» des automates cellulaires. Le problème est le suivant «Est-il possible de faire se rassembler de manière optimisée un certain nombre d’agents identiques et sans chefs répartis dans l’espace aléatoirement ?». Ce problème apparaît la première fois en 1970 lorsque l’on tente de vouloir rassembler un ensemble de robots identiques n’ayant pas de hiérarchie . Ceci est la modélisation d’une proposition de solution à ce problème. Inspiré du monde vivant et en particulier des amibes chaque agent (cellule active) déclenche de manière aléatoire une vague d’excitation qui se diffuse à la manière du modèle Réaction-Diffusion 24 Chaque agent croisant l’une de ces vagues d’information va se diriger vers la source. Malgré sa simplicité ce modèle très robuste permet de rassembler les agents de manière décentralisée même en cas d’obstacle dans l’espace ou d’asynchronisme.
[RandomWalk]
Avancé aléatoire :
Modèle permettant de tester le déplacement aléatoire d’agents parmi l’espace de simulation.
[TransactionalCA]
Onglet stochastic
[Stochastic]
Les automates cellulaires stochastiques regroupent ceux dont il n’y a pas de règle de mise a jour dans la fonction de transition. Leur évolution dépend d’éléments aléatoires. Que cela soit dans la règle de mise à jour, dans la génération d’un «bruit» dans le modèle ou bien un changement de fonctions des cellules aléatoire.
[DiploidECA]
ECA Diploid :
Dans ce modèle on prend deux ECA 25 1 et 2 mais en intégrant une probabilité «Weight(R2)» paramétrable de prendre, pour chaque cellule, comme fonction de mise a jour celui de L’ECA2 et donc une probabilité 1-«Weight(R2)» de prendre l’ECA1 .
[HardCoreNoisy]
Hard Core Noisy :
Automate cellulaire binaire en deux dimensions dont la chaque cellule va prendre aléatoirement l’état d’un de ses voisins.
[DomanyKinzel]
[RandomCopy]
Copie aléatoire :
Modèle d’automate cellulaire à n états différents représentés avec des couleurs. Chaque cellule va copier la couleur d’un de ses voisins (avec la possibilité de s’y inclure elle-même, selon le voisinage défini).
[Fusks-DensityStudy]
Etude de Fusk-Densité :
Ce modèle est une des réponses au problème de densité pour les automates cellulaires à une dimension. Le problème de densité (aussi appelé problème de la majorité) est de trouver une méthode afin qu’un système puisse parvenir a un consensus uniforme sans avoir de hiérarchie. C’est-à-dire que si dans l’espace de simulation, il y a plus de cellules à l’état 1 que de cellules à l’état 0 alors toutes les cellules doivent parvenir à l’état 1. L’inverse doit être vrai aussi. Si pour les automates cellulaires infinis 2D la réponse à ce problème est la règle de Majorité 26 avec le voisinage de Toom (Avec cette application cela ne marchera pas à tous les coups, car l’espace de simulation n’est pas infinie) il semblerait que pour les automates linéaires en 1D il n’y ait pas encore de réponses totalement déterministes. Ce modèle est donc un modèle proposant une manière stochastique (et donc non-déterministe) d’y arriver. C’est un ECA diploïde 27 prenant les règle BCFG et CDEF 28.
[Schuele]
Schuele :
Ce modèle est une des réponses au problème de densité pour les automates cellulaires à une dimension. 29 C’est un ECA diploïde prenant les règle BCFG et DE.
[TraMaj]
Trafic + Majority :
Ce modèle est une des réponses au problème de densité pour les automates cellulaires à une dimension. 30 C’est un ECA diploïde prenant les règle Traffic et Majority 31.
[GKL]
GKL :
Ce modèle est à ce moment une des réponses déterministes la plus aboutie au problème de densité pour les automates cellulaires à une dimension 32 puisque ayant un taux de réussites d’environs 80 %. La règle de mise à jour et le voisinage sont compliqués à appréhender puisqu’ils dépendent et changent en fonction de l’état de la cellule. Si la cellule est à l’état 0 alors son voisinage se compose de elle-même, son voisin de gauche et la cellule à 3 cases de distance à gauche. Si la cellule est à l’état 1 c’est la même manière de compter le voisinage mais avec la droite. Pour la fonction de transition, la cellule prend l’état majoritaire de son voisinage.
Onglet variants
[Variants]
Cet onglet contient les variantes des règles de l’automate «Game of Life»33 et d’autre automates cellulaires connus permettant d’explorer de nouveaux mécanismes avec ces derniers.
[LifeParam]
Life Parameters
Modèle totalement paramétrable permettant de tester différentes combinaisons de changement des règles du jeu de la vie:«Birth lo» et «Birth hi» définissent le nombre de voisins minimum et maximum nécessaire à une cellule pour «naître» et «Survival lo» et «Survival hi» le nombre de voisins minimum et maximum nécessaires à une cellule pour rester en vie.
[Life2Species]
Life 2 Species
Jeux de la vie mais avec deux espèces de cellule ayant deux différentes couleurs. Trois cellules jaunes donnent naissance à une cellule jaune, trois cellules vertes donnent naissance à une cellule verte. [LT-Life]
Larger Than Life
Modèle reprenant le système de vie et de mort du jeu de la vie mais en l’adaptant à un voisinage beaucoup plus grand.
Lattice-Gas Cellular Automata
Aussi appelés «LGCA» (ou Automate cellulaire de Gaz sur réseau en français). Ce terme défini les modèles d’automates cellulaires possédant un vecteur de direction dans leurs caractéristiques servant initialement à simuler des particules de gaz voyageant aux travers de canaux.
Multi-Agent
Les modèles de systèmes complexes où les cellules ne sont pas mises à jour tout les pas de temps mais par le passage d’ «agents» autonomes ayant un comportement définis.
Interacting particle
Les systèmes complexes d’interactions de particules servent à modéliser le comportement de groupe d’objet stochastique (au comportement basé sur des probabilités) interagissant ensemble. En particulier les systèmes de particules en interactions.
Description du logiciel
Le menu
Ce chapitre décrit le menu de construction d’une simulation. C’est la première fenêtre qui s’ouvre lorsqu’on lance le logiciel. Elle contient la présentation les éléments qui la composent, leurs effets et la manière de les utiliser. L’interface elle-même se compose de 7 parties (Voir figure 3.1 ) : En premier lieu (A) les onglets présentant les différents types de modèles. Ensuite (B) les listes des modèles de simulation. La partie (C) contient la description du modèle choisi. Les paramètres (D) et (E) permettent de paramétrer le modèles avant de lancer la simulation. La table de contrôle (F) contient toutes les commandes principales du menu (en particulier l’ouverture du simulateur). Enfin, la sélection de la méthode de mise à jour (G), qui n’est intéressante que dans des cas très particuliers.
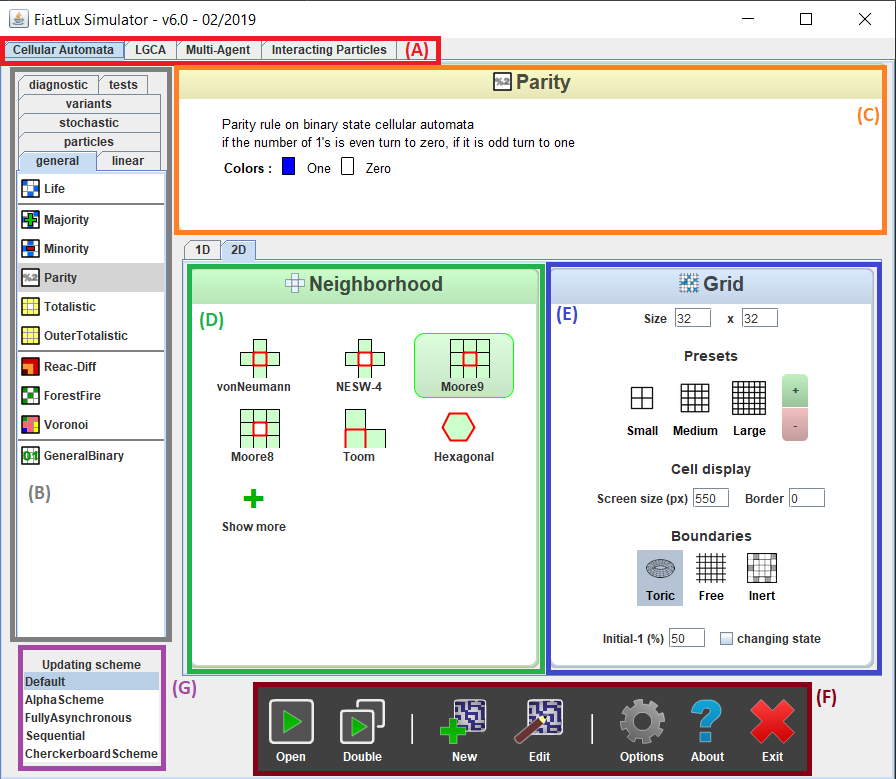
Classes de systèmes complexes
Cette liste (zone A) d’onglets contient la classification de modèle d’automate cellulaire présent dans l’application. L’utilisateur doit cliquer sur les onglets pour naviguer entre eux. Une description des modèles présents dans le logiciel se trouve au 3. Modèles .
Cellular Automata
Contenant les modèles d’automates cellulaires «standards» (Voir «[Automates cellulaires] Automates cellulaires» .).
LGCA
L’acronyme LGCA signifie «Lattice-Gas Cellular Automata» (ou Automate cellulaire de Gaz sur réseau en français). Cet onglet contient les modèles d’automates cellulaires possédants, en plus de leur état, un vecteur de direction dans leurs caractéristiques.
Multi-Agent
Contiens les modèles de systèmes complexes où les cellules ne sont pas mises à jour tous les pas de temps mais par des «agents» autonomes ayant un comportement défini.
Interacting particles systems
Les systèmes complexes d’interactions de particules servent à modéliser le comportement de groupes d’objets stochastiques (au comportement probabiliste) interagissant ensemble. En particulier les systèmes de particules en interactions.
Les modèles
Dans chaque onglet type se trouve à gauche dans la fenêtre une liste de modèles (qui peut elle-même être redivisée en onglets) ayant chacun un nom et une icône. Cliquer sur un modèle de cette liste afin de le sélectionner fera alors apparaitre une description du modèle au centre de l’interface. (Sur la figure [le menu lors du lancement de l’application] , le modèle «Parity» est sélectionné)
Une description des modèles présents dans le logiciel se trouve au 3. Modèles .
Les paramètres de modélisation
Au centre de l’interface apparaissent les paramètres de modélisation servant à définir les simulations du modèle sélectionné. Divisé en deux menus (sauf pour les modèles LGCA qui ne possèdent que les paramétrage de Grid), le premier pour définir la fonction de voisinage des cellules et le second pour paramétrer l’espace de simulation :
[Neighbourhood]
Neighbourhood
Ce menu contient les différents moyens de définir le voisinage des cellules du modèle. Il faut cliquer sur l’un des schémas pour sélectionner:
Voisinage à une dimension
LineR
Ces voisinages prennent en compte l’état de la cellule centrale et les états des N cellules sur les deux cotés de la cellule centrale. N étant le nombre noté dans le nom du voisinage «LineR-N».
LineA
Ces voisinages prennent en compte l’état de la cellule centrale et les états des cellules prisent en compte dans les coordonnés [min,max] l’origine étant la cellule centrale. Ainsi «LineA[-1,2]» prend en compte la cellule juste à gauche et les deux à droite de la cellule centrale.
GKL
Voisinage changeant en fonction de l’état de la cellule principale: Si la cellule est à l’état 0 alors son voisinage se compose de elle-même, son voisin de gauche et la cellule à 3 cases de distance à gauche. Si la cellule est à l’état 1 c’est la même manière de compter le voisinage mais avec la droite.
Custom1D
N’est pas fonctionnel pour le moment.
Voisinage à deux dimensions
vonNeumann
Voisinage prenant en compte l’état de la cellule et des 4 cellules la juxtaposant directement.
NESW-4
Voisinage prenant en compte les états des 4 cellules juxtaposant directement la cellule principale sans prendre cette dernière en compte.
Moore9
Voisinage prenant en compte l’état de la cellule et des 8 cellules la juxtaposant directement.
Moore8
Voisinage prenant en compte les états des 8 cellules juxtaposant directement la cellule principale sans prendre cette dernière en compte.
Toom
Voisinage prenant en compte l’état de la cellule et des 2 cellules la juxtaposant directement en haut et à gauche.
Hexagonal
Ce voisinage change la topologie de l’espace: Au lieu que les cellules soient des carrés ayant 4 ou 8 voisins avec cette configuration les cellules seront des hexagones ayant 6 voisins et ne prend en compte que les états des voisins directes.
Grid
Permet de paramétrer la grille utilisée lors de la simulation :
Taille de la grille
Size
Permet de paramétrer la résolution de l’espace. L’unité est en nombres de cellules. Pour les automates cellulaires en deux dimensions l’utilisateur peut cliquer sur un nombre et changer la valeur afin de mettre la taille à votre convenance. Pour les automates en 1D la valeur est à changer dans l’encadré «N cells» pour «Nombre de cellules». Toujours pour les automates à une dimension, un paramètre «Buffer» donne la configuration qui seront gardées dans l’historique et affichées lors de la simulation.
Presets
Présente trois réglages par défaut, cliquer dessus afin de mettre à jour la taille de la grille (la taille apparaitra dans la partie «size») :
Small
Taille de la grille à 4 x 4 cases.
Medium
Taille de la grille à 32 x 32 cases.
Large
Taille de la grille à 100 x 100 cases.
Radio buttons
Des boutons «+ / -» sont aussi affichés sur l’interface et permettent de multiplier ou de diviser par deux la taille de la grille (qui apparait dans la partie «Size»).
Paramétrage des cellules
Il est possible de paramétrer la taille en pixels maximale que prendra la grille dans la simulation dans la partie «Cell display».
La valeur «Border» est le nombre de pixels noirs qui délimiteront les cellules de la grille. Par défaut celui-ci est donné 0 et la valeur 1 est conseillée pour afficher les limites des cellules.
Boundaries
La partie «Boundary» définit le comportement de la simulation pour les bords de la grille. Le logiciel propose trois types de bords :
Toric
Les cellules qui seront à un bord de la grille auront comme voisines celles qui seront à l’opposées. L’espace du modèle prend donc la forme d’un tore pour les modèles 2D et d’un cylindre pour les modèles 1D. Par exemple, dans un modèle en 2D, une cellule tout en haut de la grille sera considérée comme voisine de celle à l’opposé tout en bas.
Free
Le paramètre «free» représente un univers fini et limité où les cellules aux bords de la grille n’ont pas de voisines.
Inert
Avec la configuration «Inert» les cellules aux bords de l’espace de simulation ont leurs propres fonctions de mise à jour. Cela signifie que les cellules aux extrémités de la simulation seront générées lors de l’initialisation au même titre que les cellules au centre (avec le pourcentage défini dans State initial-1 1.3.2.4 ) mais durant la simulation leurs états ne varieront soit pas au cours du temps soit avec une probabilité de 1/2 peu importe leur voisinage34.
State
Les deux paramètres «State» ne s’appliquent que pour les conditions aux bords de type «inert».
Initial-1:
Représente la probabilité d’être à l’état 1 pour les cellules aux bords de l’espace lors de l’initialisation de la simulation. (par défaut à 50 [changingState]
Changing state:
Si coché, les cellules du bords changeront leur état avec probabilité 1/2 à chaque pas de temps.
Table de contrôle
En bas de le menu (F) se trouve la barre de fonctionnalités en sombre ayant plusieurs boutons renvoyant vers diverses fonctionnalités.
Lancement du simulateur
Open
Ouvre une fenêtre de simulation du modèle sélectionné avec les paramètres choisis précédemment35.
Double
Seulement présent pour les modèles se trouvant dans l’onglet «Cellular Automata», ouvre un simulateur en mode dit de «couplage» qui permet d’observer des comparaisons entre deux simulations.
Édition de modèles
Attention
Disponible uniquement pour les modèles présents dans l’onglet «Cellular Automata»!
New
Ouvre une interface de création d’un nouveau modèle vous demandant de choisir entre trois type de création de modèles avant de vous renvoyer vers l’interface d’édition de modèle.
Edit
Lance l’éditeur du modèle sélectionné.
Contrôles
Options
Ouvre une fenêtre contextuelle (pop-up) permettant d’accéder aux options de l’application. Pour le moment une seule option est disponible :
Save
Par défaut les valeurs rentrées dans les configurations (autres que les éditions et créations de modèles) ne sont pas sauvegardées et sont donc remises à leurs états initiales au lancement de l’application. En cliquant sur «Save» l’utilisateur peut retrouver ses paramètres lors des prochains lancements.
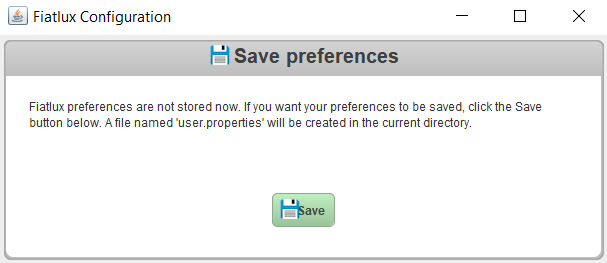
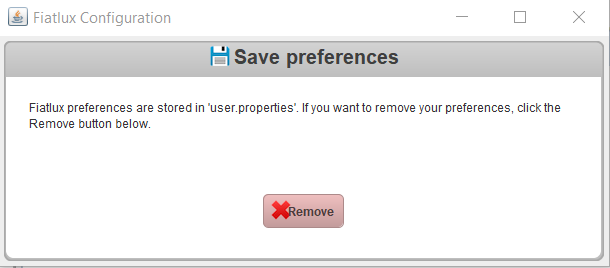
Remove
Il est possible de rétablir les paramètres initiaux en supprimant les préférences personnelle en cliquant sur «Remove».
About
Le bouton «about» permet d’avoir des informations sur le logiciel tel que sa version, sa date de dernière mise à jour, son concepteur, la licence de distribution, un accès au site web, a la documentation et avoir un contact pour envoyer un retour sur cette application.
Close
Ferme la totalité de l’application.
Attention :
Fermer le menu entrainera la fermeture de l’application et de l’ensemble des fenêtres du logiciel et les progressions non-sauvegardés seront perdues!
Simulateur
Le simulateur apparait lorsque l’utilisateur «ouvre» une fenêtre de simulation pour un modèle36. C’est une interface divisée en quatre espaces : Le Viewer de la simulation qui contient l’affichage de la simulation en cours, la table de contrôle (affichée en bas de l’interface) du simulateur permettant de diriger la simulation. Une partie sur la droite contenant plusieurs fenêtres d’outils. Et enfin une partie grisée (et optionnelle) au-dessus pour les options paramétrables du modèle choisis.
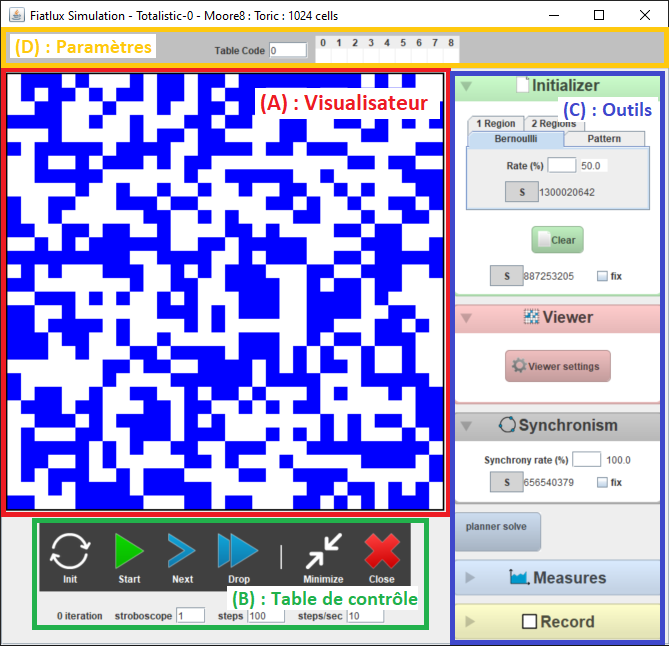
Visualiseur
Au centre de l’interface se trouve le visualiseur de la simulation. Il prend la taille donnée dans les paramètres de grille37 lors de l’ouverture du simulateur. Certains modèles acceptent que l’utilisateur puisse intervenir dans la simulation en temps réel. Si c’est le cas, l’utilisateur peut cliquer sur des cellules afin de changer leurs états. Il est possible de changer des paramètres du visualiseur si le modèle le permet tel que le déplacement de l’origine par exemple dans la zone des outils : «Viewer».
Table de contrôle
En bas de l’interface du simulateur se trouve la barre de contrôle (affichée même dans un simulateur minimisé) avec ses paramètres et ses informations en dessous d’elle (qui eux ne sont pas affichés dans la fenêtre minimisée). La barre elle-même est divisée en deux séparant par un trait les fonctionnalités qui agissent sur la simulation et celles sur l’interface.
Fonctionnalités de simulation
Init
Le bouton d’Initialisation permet d’initialiser la simulation en utilisant l’Initialiseur38 choisi. Il remet aussi le compteur d’initialisation à 0 et change les clés aléatoires si elles n’ont pas été «fixées».
Start / Stop
Le bouton «Start» lance la simulation au rythme défini par le paramètre «step/sec» et «stroboscope». Une fois la simulation lancée le bouton change pour devenir «Stop» avec le symbole de pause. Cliquer dessus mettra alors la simulation en suspension. Le bouton redeviendra «Start» avec le triangle vert permettant la reprise de la simulation. Durant le moment de pause il est toujours possible de faire progresser la simulation avec «Next» et «Drop».
Next
Le bouton «Suivant» fait avancer la simulation d’un pas de temps. Action répétable indéfiniment.
Drop
Le bouton «Drop» fait faire un saut à la simulation la faisant avancer d’un certain nombre de pas de temps définis par le paramètre «steps».
Fonctionnalités du simulateurs
Minimize
Le bouton «Minimize» diminue la taille de la fenêtre du simulateur, lui donne un fond sombre et occulte les paramètre de la table de contrôle et les outils. Il permet d’afficher la simulation dans une interface plus petite. Seuls les paramètres du modèle, la simulation, la table de contrôle avec son compteur d’itération reste alors visible. Si le mode «diminué» de l’interface est activée alors le bouton est remplacé par un carré blanc permettant de ré-afficher toutes les informations de l’interface.
Close
Ferme l’interface et la simulation en cours.
Informations et paramètres
Compteur d’itérations
Compte le nombre de pas de temps effectués depuis la dernière initialisation de la simulation. S’initialise à 0 lors d’une initialisation (clic sur le bouton «Init») ou lors d’un clic sur le bouton «Clear» de l’initialiseur.
Stroboscope
Par défaut avec une valeur de 1, le paramètre «stroboscope» indique le nombre de pas de temps effectués entre deux affichages de l’état simulation.
Steps
Steps indique le nombre d’itérations effectués d’un coup lorsque l’on utilise le bouton «Drop». Initialement à la valeur de 100, si l’utilisateur clique sur «Drop» la simulation fera une avancée de 100 pas de temps.
Steps/sec
Paramètre indiquant le nombre d’avancées de pas de temps que la simulation effectue chaque seconde une fois lancée via le bouton «Start». Cette valeur est un maximum : si l’ordinateur ne peut suivre la cadence donnée le logiciel affichera un maximum d’itérations possible dans la seconde.
Outils
Les outils contiennent, séparés en zones dédiés à chaque partie de la simulation, les paramètres et les fonctionnalités sur lesquels l’utilisateur peut adapter ses simulations afin qu’elles correspondent un maximum à ses besoins.
Initializer
La partie «Initializer» présente les différents moyens d’initialiser la simulation. Les méthodes diffèrent suivant les modèles. Les différentes possibilités sont présentées ci-dessous.
Standard
Initialiseur des modèles ayant une initialisation binaire, soit la plupart des modèles présents dans «Cellular Automata» onglet «general» et «linear» il se découpe en quatre différentes méthodes de mise à jour :
Bernoulli
Donne le pourcentage, pour chaque cellule d’être à l’état actif lors de l’initialisation de la simulation. Il vient avec une graine aléatoire39.
Pattern
Dans ce champ de texte il est possible de rentrer un paterne binaire (exemple : «100») pour que, lors de l’initialisation de la simulation, l’état initial de l’espace soit une répétition du paterne demandé (dans notre exemple il y aurait donc une cellule active puis deux cellules inactives, puis une cellule actives, et ainsi de suite).
Viewer
La zone «Viewer» contient les paramètres du visualiseur de la simulation. Les deux les plus communs sont pour les modèles en 1D et 2D de l’onglet «cellular automata» et qui sont présentés ci-dessous :
Viewer – Automate cellulaire à une dimension
buffer period
La zone «Viewer» pour les automates cellulaires à une dimension contient un premier paramètre nommé «buffer period» est initialement à 1 et représente le nombre de pas de temps effectués sur une ligne de la simulation avant que celle-ci ne soit enregistrée et que la simulation passe à la suivante. Cela veut dire que, par défaut, à chaque pas de temps la simulation passe a la ligne suivante. Si le paramètre était défini à 5 par exemple cela voudrait dire que la simulation avancerait de 5 itérations avant de passer à la ligne suivante.
Radar mode
Si désactivé (par défaut) chaque nouvel enregistrement de l’espace prendra la place du dessus du visualiseur de la simulation et décalera les autres enregistrements vers le bas. Si le mode radar est activé alors chaque enregistrement de l’espace se fera en traversant le visualiseur de la simulation de haut en bas et s’enregistrera «par-dessus» en écrasant la dernière sauvegarde se trouvant à cet endroit.
shift
Représente un mouvement de translation. Initialement à 0, les cellules se décaleront d’autant de cases à chaque pas de temps si une valeur (positive ou négative) est rentrée.
Viewer – Automate cellulaire à deux dimensions
Pour les automates cellulaires en deux dimensions la zone se compose d’un bouton permettant d’afficher une nouvelle fenêtre contenant les paramètres du visualiseur :
stability
Les cellules instables sont définies comme étant celles qui changeront d’état lors de leur prochaine mise à jour. Si le bouton «stability» est coché sur On alors les cellules instables seront marqués d’un point noir.
Déplacement de l’origine
Les deux variables «DX» et «DY» (pour déplacement en X/Y) sont initialement à 0. Si une valeur est entrée alors a chaque pas de temps le visualiseur de la simulation se déplacera d’autant de cellules sur l’axe rentré. Le mouvement est constant et si les valeurs sont changées alors l’origine retourne à sa place initiale.
Synchronism
Cette zone-ci contient un paramètre et une graine aléatoire40. Le paramètre, nommé «synchrony rate» (soit «taux de synchronisme» en français) est par défaut à 100. Cette variable représente la probabilité de chance, pour chaque cellule, de se mettre à jour lors de la prochaine itération. Par défaut chaque cellule se met à jour à chaque itération (100 % de synchronicité). Si le taux est rentré à 50% alors, à chaque pas de temps, chaque cellule à autant de chance de se mettre à jour. Si elle n’est pas mise à jour une cellule ne fait que «passer son tour» et son état ne change pas.
Cas spéciaux:
Certaines valeurs de ce taux de synchronicité déclenche d’autre comportement permettant d’étudier le bruit dans les modèles d’automates cellulaires. Voici une liste des taux à donner afin d’y avoir accès :
- 0
-
Si cette valeur est utilisée comme taux de synchronisme la simulation prendra une cellule aléatoirement et la mettra à jour. Ce mode recommence ce processus n fois (où n est le nombre de cellules dans l’espace) par pas de temps.
- -1
-
Avec cette valeur à chaque pas de temps c’est une seule cellule choisie aléatoirement qui sera mise à jour.
Measures
La zone servant à prendre des mesures de la simulation en cours. Suivant les modèles différents type de rapports sont proposés. À gauche de cette fenêtre se trouve les différentes variables qu’il est possible de mesurer et à droite les boutons représentant les différentes options des mesures de modèles. Afin de pouvoir utiliser les outils de mesures il faut d’abord sélectionner la variable que l’utilisateur souhaite mesurer. En cliquant dessus la variable s’affiche sur fond bleu. Une fois sélectionnée cliquer sur le bouton pour choisir le mode de mesure voulus.
Variables
Densité
La densité donne le ratio des cellules n’étant pas à l’état 0.
Activité
«activity» représente le ratio de cellules changeant d’états a chaque avancé de pas de temps. Cela permet de quantifier les évolutions que connaît la simulation.
Mode de mesure
Diagramme
«Open Plot» ouvre une nouvelle fenêtre représentant une courbe représentant l’évolution de la variable sélectionnée sur le temps. Ce diagramme se met à jour automatiquement avec le temps.
Quatre boutons sont présents dans l’interface de la courbe en haut à droite. De gauche à droite, le premier, représentant une photocopieuse permet d’imprimer ou de sauvegarder la courbe obtenue à l’état actuel. Le second, contenant une flèche bleue permet de rendre illisible la courbe (Une correction de ce bug arrive dans une prochaine version). Le troisième, qui montre deux points rouges de la courbe, ouvre une autre interface permettant de personnaliser la courbe (Nom des abscisses/ordonnées, taille de la grille, forme des points…). Le dernier, avec des bords gris permet d’adapter le visualisateur de la courbe afin d’avoir une meilleure visualisation de celle-ci.
Record
Permet d’enregistrer l’état actuel du système. Il y a 4 formats pris en compte pour l’instant : PNG, TXT, BMP et SVG. Attention néanmoins : le format SVG ne fonctionne pas et utiliser le format TXT fera crasher le logiciel. Un correctif sera apporté dans une prochaine mise à jour de FiatLux. Les sauvegardes sont enregistrées avec un nom suivant un modèle comme présenté ici :
NomDuModele-0-Suffixe-t+NumeroDeLIteration.Format
Le suffixe est modifiable en remplissant le paramètre suffix. La case à cocher « Rec » fait un enregistrement continu : chaque itération sera enregistrée automatiquement. Si la case « Print Source » est cochée alors pour chaque enregistrement fait un fichier sans format sera sauvegardé aussi. Ce fichier contiendra l’état de l’espace sous forme d’une suite de chiffres.
Paramètres
En zone grisée au-dessus de la fenêtre du simulateur se trouvent les paramètres que certain modèles proposent. Les différents paramètres proposés par modèle sont décrits dans la partie 3 Description des modèles .
La plupart des options sont des champs de texte ou de nombres. Il faut cliquer dessus, rentrer la valeur voulue et appuyer sur entrée pour enregistrer le nouveau paramètre. La valeur est alors affichée à côté du champ à remplir.
Il est aussi possible que certaines options soient sous la forme d’un tableau à cocher. Cliquer sur la cellule du tableau afin de changer sa valeur le changement est alors immédiatement enregistrée.
Enfin, si de l’aléatoire est utilisée dans les options alors est affichés une clé aléatoire41 (délimité par un «S» grisé) avec un bouton dit «checkbox» pour «fixer» la clé et ne pas la changer lors de la prochaine initialisation.
Les graines aléatoire
A chaque endroit où de l’aléatoire est présent dans le logiciel l’utilisateur peut gérer les graines aléatoires. Elles se composent d’un cadre grisé contenant un S, un bouton à cocher « fix » et de la valeur de la graine entre les deux. Le principe derrière cela est que si la clé aléatoire est la même alors le logiciel produira les même comportements.
En cliquant sur le S grisé l’utilisateur peut rentrer la valeur d’une clé qu’il connaît. La valeur même de la clé est générée a chaque initialisation de la simulation en cliquant sur le bouton Init ou Clear par exemple. En cochant le bouton fix la clé ne changera plus lors de l’initialisation.
Un exemple :
Dans l’initializer j’ai la clé « 236181430 » si j’initialise encore une fois ma simulation la valeur de la clé changera et les cellules générées ne seront plus les mêmes. Si je clique sur le S grisé alors je pourrais rentrer la valeur de cette clé et lors de l’initialisation je retrouverai la même génération de cellules que la première fois. Si je veux conserver cette génération je peux cocher fix afin que la valeur ne change plus et conserver ma génération.
-
Voir [Neighbourhood]. Neighbourhood .↩︎
-
Dans la partie 3 Modeles présents se trouvent les paramètres que contiennent les modèles.↩︎
-
Voir [Neighbourhood]. Neighbourhood .↩︎
-
Voir [DiploidECA]. Dilpoïd Elementary Cellular Automata .↩︎
-
Voir [React-Diff]. Réaction-Diffusion .↩︎
-
Voir [Majority]. Majority .↩︎
-
Voir [DiploidECA]. ECA Diploïde .↩︎
-
Pour voir cette notation des règles ECAs voir [ECA Tableau de transition]. ECA – Notation de transition page↩︎
-
Pour voir le problème de la densité voir [Fusks-DensityStudy]. Etude de densité Fusk .↩︎
-
Pour voir le problème de la densité voir [Fusks-DensityStudy]. Etude de densité Fusk page↩︎
-
Pour voir ces règles ECAs voir [ECAsInterressants]. ECA – Règles intéressantes .↩︎
-
Pour voir le problème de la densité voir [Fusks-DensityStudy]. Etude de densité Fusk page↩︎
-
Voir [changingState]. Changing state .↩︎