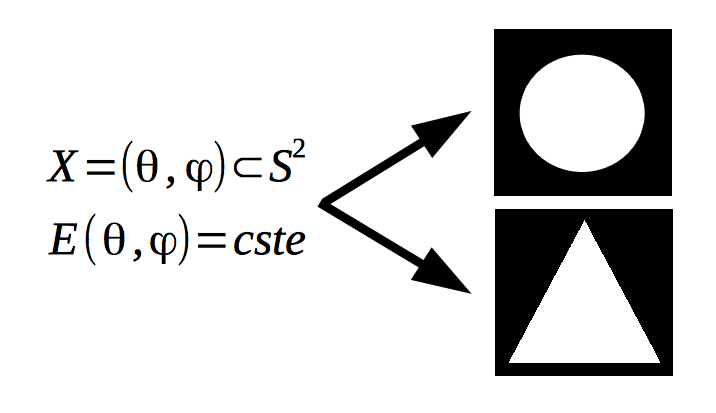
Here are test cases of simulated reflectors with blender and a comparison between solvers.
-
PIR0
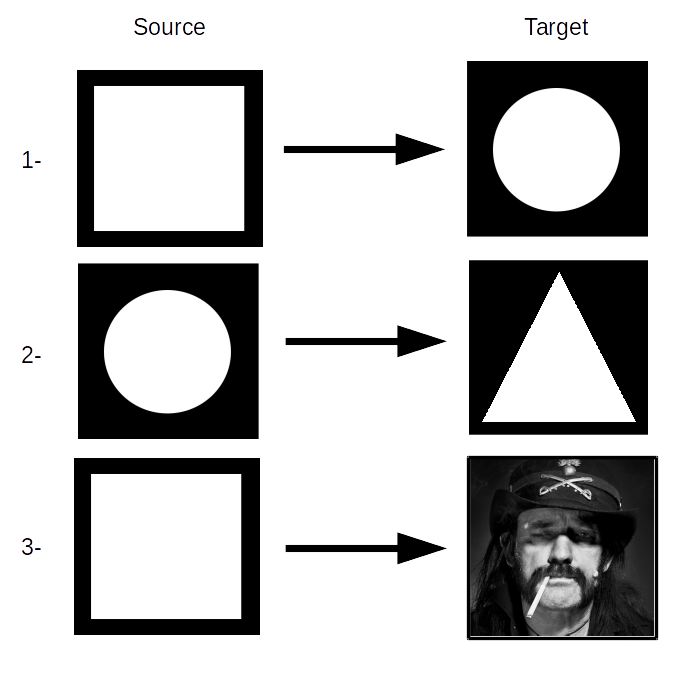
Three test cases for PIR0. 1- Uniform square to uniform disc. 2- Uniform disc to uniform triangle. 3- Uniform square to Lemmy Kilmister portrait.
Keeping the notations of the PIR0 configuration schematic, the geometrical configuration is as follow:
\(\displaystyle \vec{s_1} = \begin{pmatrix} 1\\0\\0 \end{pmatrix}, \ \ \ \vec{e_{\eta}} = \begin{pmatrix} 0\\-1\\0 \end{pmatrix}, \ \ \ \vec{e_{\xi}} = \begin{pmatrix} 0\\0\\1 \end{pmatrix}, \ \ \ \vec{n_{p}} = \begin{pmatrix} -5000\\0\\0 \end{pmatrix}\)
The source support is \(\displaystyle [-5, 5]\times[-5,5]\) and the target plan support is \(\displaystyle [-500, 500]\times[-500,500]\).
It is important to choose a large \(\displaystyle \| \vec{n_p}\|\) and a large target plan support compared to the source support to ensure correct far-field conditions, otherwise deformations will occur at the rendering step.

Results of the reflector simulation with Blender. First column is IPFP, second is Semi-Discrete and third is Finite differences. Below each picture are the source and target resolution and the execution time.
-
PIR1
The geometrical configuration in these cases is as follow:
\(\displaystyle \vec{s_1} = \begin{pmatrix} 1\\0\\0 \end{pmatrix}, \ \ \ \vec{e_{\eta}} = \begin{pmatrix} 0\\-1\\0 \end{pmatrix}, \ \ \ \vec{e_{\xi}} = \begin{pmatrix} 0\\0\\1 \end{pmatrix}, \ \ \ \vec{n_{p}} = \begin{pmatrix} -500\\0\\0 \end{pmatrix}\)
The source opening angle is \(\displaystyle \frac{\pi}{20}\) and the target plan support is \(\displaystyle [-50, 50]\times[-50,50]\).
As describe in the Solver part of Numerical Methods, the optimized version of the IPFP algorithm is not available yet, explaining the very long execution time compared to PIR0.