Information-Theoretic bounds for Regression
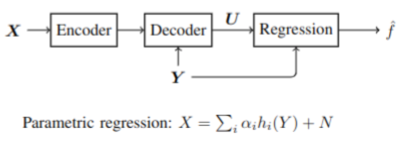
In the context of goal-oriented communications, we consider that a source is compressed and transmitted to a receiver which aims to perform a regression using both the received compressed data and the side information available only at decoder, as illustrated in the coding scheme.
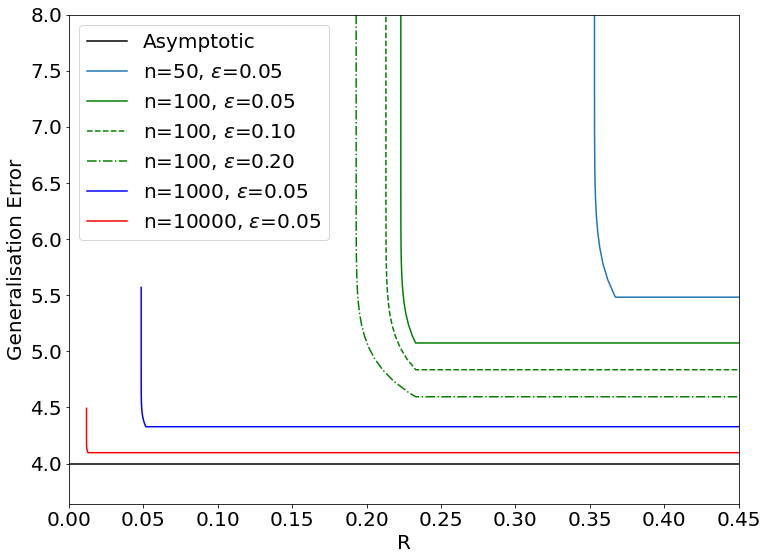
For parametric regression performed on compressed observations, we derive new achievable Information-Theoretic (Rate, Generalization Error) regions in an asymptotic regime, and show that the proposed bounds are much tighter than existing ones. This result is then extended to a non-asymptotic regime using tools from finite block-length information-theory.
We next investigate the trade-off between the data reconstruction evaluated from the distortion, and the regression task evaluated from the generalization error. Existing works show that for various learning tasks (hypothesis testing, visual perception, etc.), there is a tradeoff in terms of coding rate between reconstruction and learning performance. In the case of regression, we propose an achievable scheme to asymptotically achieve both the minimum generalization error and optimal reconstruction rate-distortion region, which shows that there is actually no trade-off between reconstruction and regression. We also confirm this result in a non-asymptotic regime, by evaluating the correlation between the different terms of the dispersion matrix.
[1] M. Raginsky, “Learning from compressed observations,” in 2007 IEEE Information Theory Workshop, 2007, pp. 420–425.
[2] S. Watanabe, S. Kuzuoka, and V. Y. F. Tan, “Nonasymptotic and second-order achievability bounds for coding with side-information,” IEEE Transactions on Information Theory, vol. 61, no. 4, pp. 1574–1605, 2015
[3] Y. Blau and T. Michaeli, “Rethinking lossy compression: The rate-distortion-perception tradeoff,” in International Conference on Machine Learning. PMLR, 2019, pp. 675–685.
[4] G. Katz, P. Piantanida, and M. Debbah, “Distributed binary detection with lossy data compression,” IEEE Transactions on information Theory, vol. 63, no. 8, pp. 5207–5227, 2017
Learning on entropy-coded images with CNN
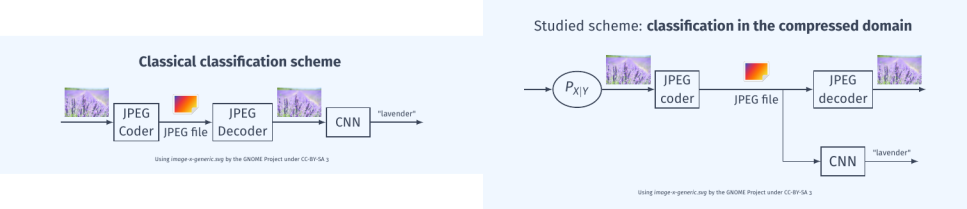
We start from the observation that the volumes of generated visual data are so massive (500 hours per minute uploaded to YouTube in 2022) that these data cannot be viewed by humans but rather by machines. For tasks performed by these machines (object detection, tracking, scene recognition, etc.), the reconstruction of the entire image is not necessary. Therefore, we are interested in the question of processing data directly in the compressed domain, specifically within the binary stream generated by an encoder that includes an entropy coding function.
In fact, in data compression algorithms (such as JPEG, MPEG, etc.), entropy coding is the only operation that reduces the size of the data, while other operations (transform, prediction) prepare the data but do not reduce its size. Thus, we study the issue of classification in the entropy-compressed domain when this classification is performed using a CNN, which is one of the most advanced methods in the state of the art.
The question is challenging due to the characteristics of entropy codes, where the encoded symbols have variable sizes and the coding function is not fixed but depends on the data. The contributions are manifold:
- Contrary to intuition, we demonstrate that it is possible to learn from entropy-coded data (with an expected loss of performance).
- We propose two properties that are necessary for a convolutional neural network to perform well.
- This qualitatively explains the loss of performance when dealing with data in compressed form.
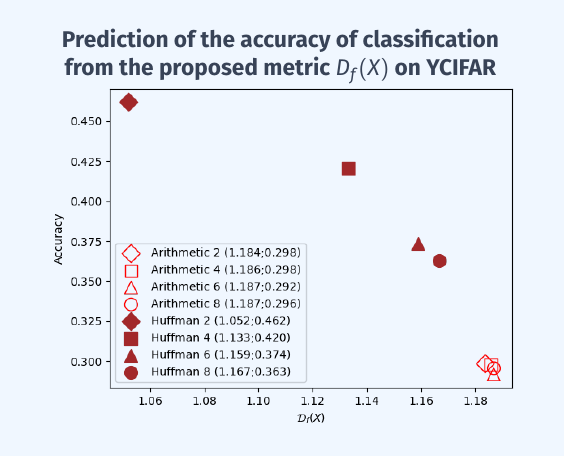
- We introduce a metric (quantitative this time) that allows us to predict the loss of performance when data is entropy-coded.