Optimal Transport and flows in probability space
In the context of this project, we are interested in understanding the flows of information in machine learning methods such as deep learning. We started by examining and studying methods such as normalizing flows, that allow to transport an unknown probability distribution onto a a simpler, parametric one, such as a Gaussian, with a tractable likelihood. We then naturally extend this study to optimal transport, which provides a natural framework for expressing such operations. As one of our goal was to consider tranfser between incomparable spaces, we first examined Gromov-Wasserstein distances, for which we deisgned efficient computation algorithm based on subspace projections (detours). We then switched to gradient flows in probability spaces, where we designed a fast solver based on sliced version of the optimal transport (Wasserstein) distance.
https://arxiv.org/abs/2110.10932
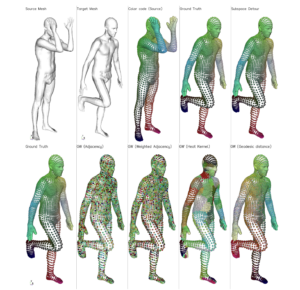
In the context of optimal transport methods, the subspace detour approach was recently presented by Muzellec and Cuturi (2019). It consists in building a nearly optimal transport plan in the measures space from an optimal transport plan in a wisely chosen subspace, onto which the original measures are projected. The contribution of this work is to extend this category of methods to the Gromov-Wasserstein problem, which is a particular type of transport distance involving the inner geometry of the compared distributions. After deriving the associated formalism and properties, we also discuss a specific cost for which we can show connections with the Knothe-Rosenblatt rearrangement. We finally give an experimental illustration on a shape matching problem.
Sliced-Wasserstein Gradient Flows
https://arxiv.org/abs/2110.10972
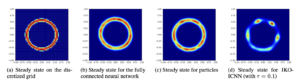
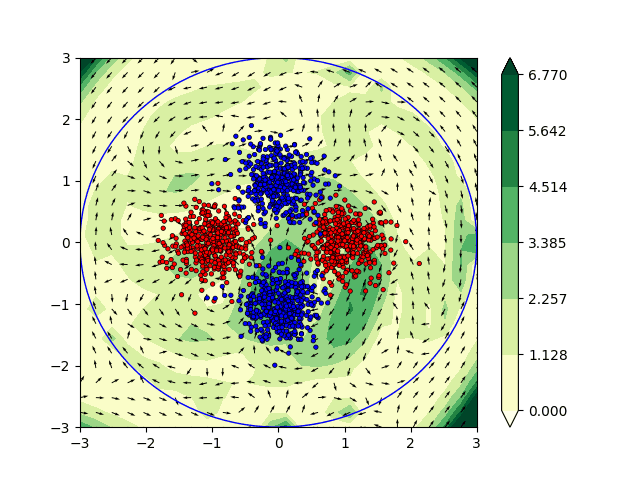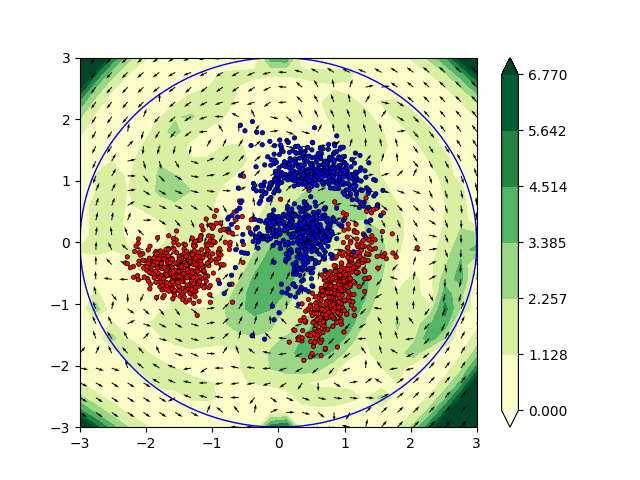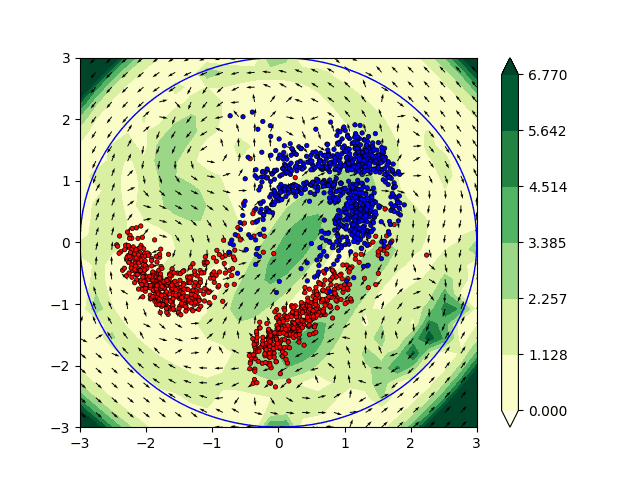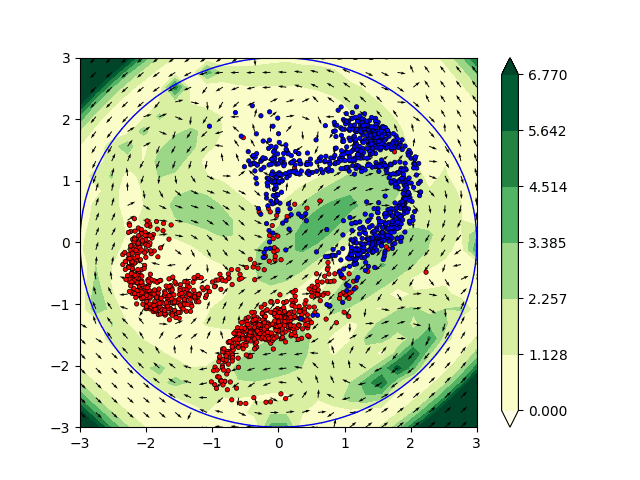
Minimizing functionals in the space of probability distributions can be done with Wasserstein gradient flows. To solve them numerically, a possible approach is to rely on the Jordan-Kinderlehrer-Otto (JKO) scheme which is analogous to the proximal scheme in Euclidean spaces. However, it requires solving a nested optimization problem at each iteration, and is known for its computational challenges, especially in high dimension. To alleviate it, very recent works propose to approximate the JKO scheme leveraging Brenier’s theorem, and using gradients of Input Convex Neural Networks to parameterize the density (JKO-ICNN). However, this method comes with a high computational cost and stability issues. Instead, this work proposes to use gradient flows in the space of probability measures endowed with the sliced-Wasserstein (SW) distance. We argue that this method is more flexible than JKO-ICNN, since SW enjoys a closed-form differentiable approximation. Thus, the density at each step can be parameterized by any generative model which alleviates the computational burden and makes it tractable in higher dimensions.
Super-resolution in Physical Imaging
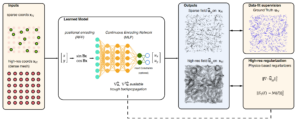
We have worked on the reconstruction of high dimensional turbulent fields from sparse low resolution measurements. This task, crucial in many applications spanning from geoscience to compute vision and medicine, has recently been addressed with fully convolutional deep neural network models. Though efficient, they suffer from a lack of physical consistency and they require spatial data and a large number of pairs for training. This is sometimes incompatible with practical data (sparse like in Particle Tracking Velocimetry, or few fully resolved data in Direct Numerical Simulations). We have worked on the use of small neural networks, trained only using location coordinates and that estimate the underlying function to reconstruct the velocity. Once trained, the reconstruction at any resolution can be performed. We have explore the reconstruction using various basis (random fourier in particular) coupled with physics-based soft and hard constraints intended to minimize PDEs residuals. This work has started with Diego di Carlo’s post doc and has recently been accepted in the Laser conference (see publications).
Euler equations and learning
We have also worked on the incorporation of some physical constraints directly in machine learning (ML) algorithms. In particular we have focused our attention on the Euler’s equations which are widely used in fluid dynamics. From a non physical perspective the solutions to the Euler’s equation are geodesics in the space of volume preserving diffeomorphisms [Arnold 66]. The computation of geodesics are of particular interest in ML applications. They can be interpreted as the shortest path between the initial state and the output of the network allowing theoretical guarantees and a better understanding of the architecture. In practice we have investigated the interpretation of ML algorithms as dynamical systems satisfying the Euler’s equations. This framework has been applied to solve various classification problems in two dimensions. This promising approach is currently being studied to combine Euler’s equations and the OT approach described previously