 Effectivity indices, smooth solution, geometric V-multigrid |
 Effectivity indices, singular solution, preconditioned conjugate gradients |
 Total error distribution |
 Total estimator distribution |
 Algebraic error distribution |
 Algebraic estimator distribution |
 Total misfit for a global stopping criterion: the shape is determined by algebra |
 Algebraic misfit for the global stopping criterion |
 Total misfit for a local stopping criterion: the shape is determined by discretization |
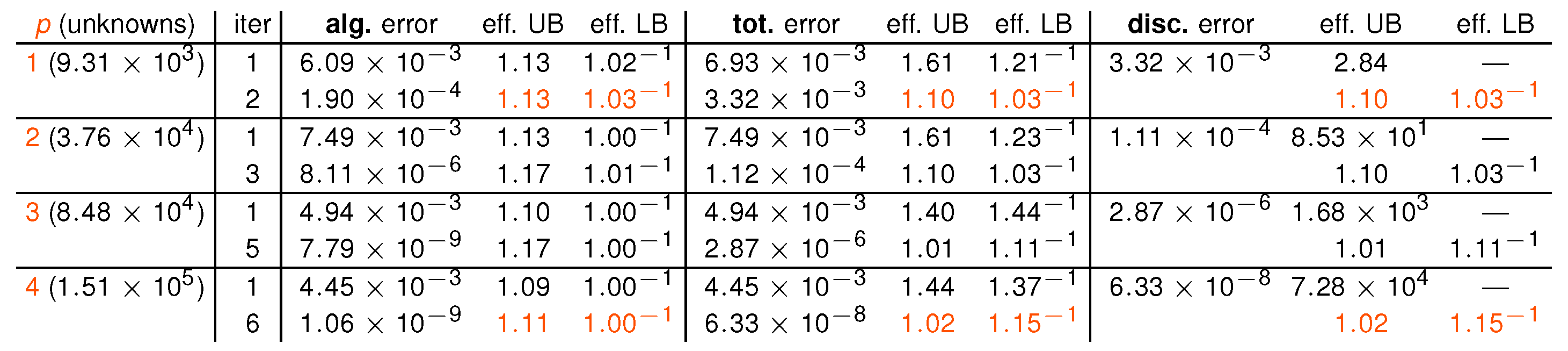
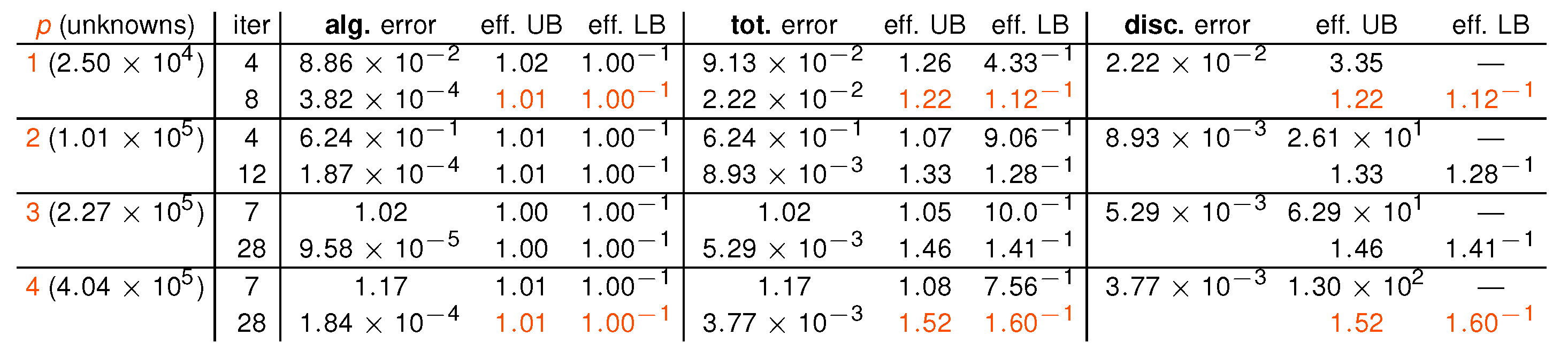
Main results:
- total, algebraic, and discretization errors: guaranteed upper and lower bounds;
- valid for arbitrary iterative algebraic solver;
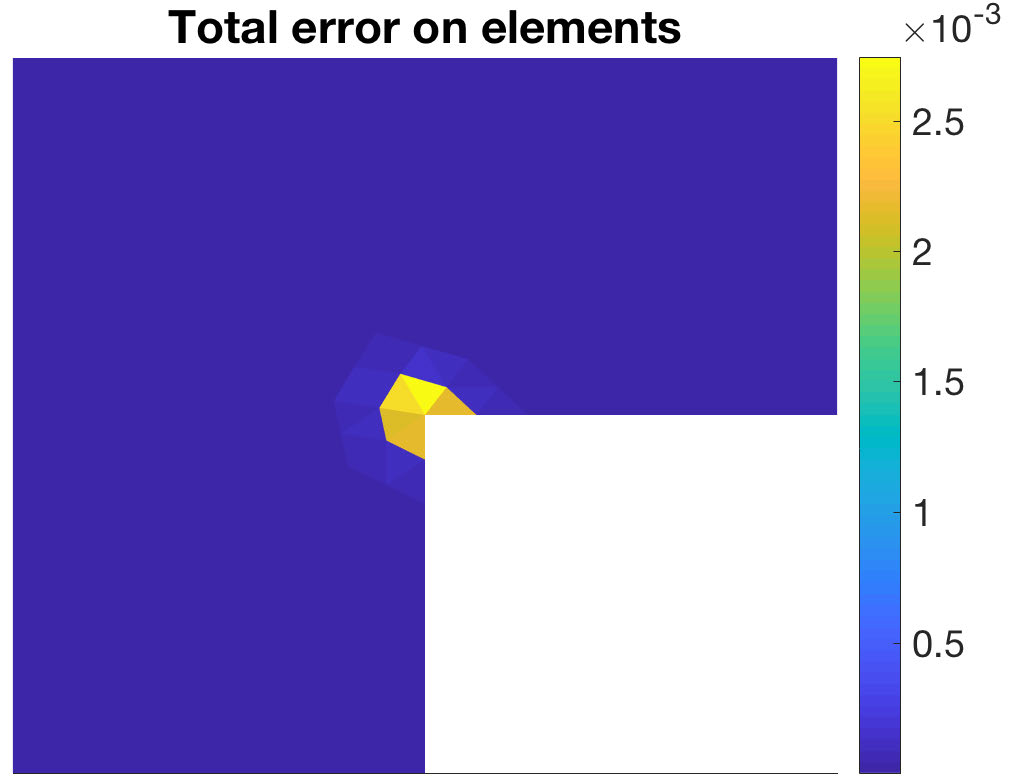
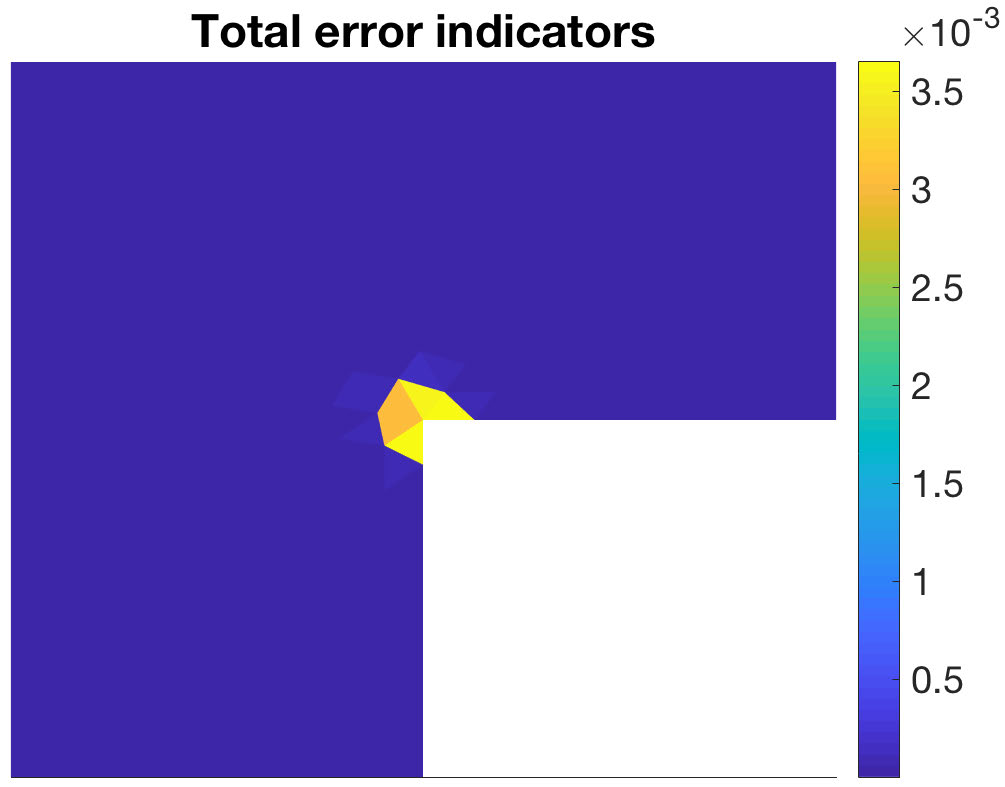
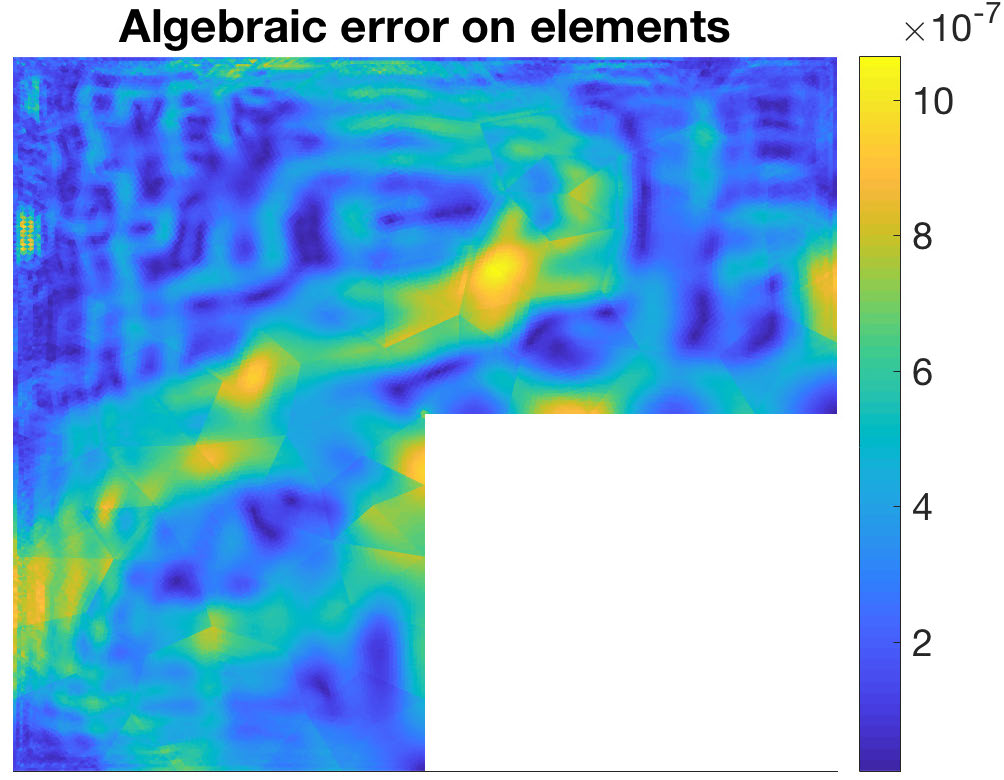
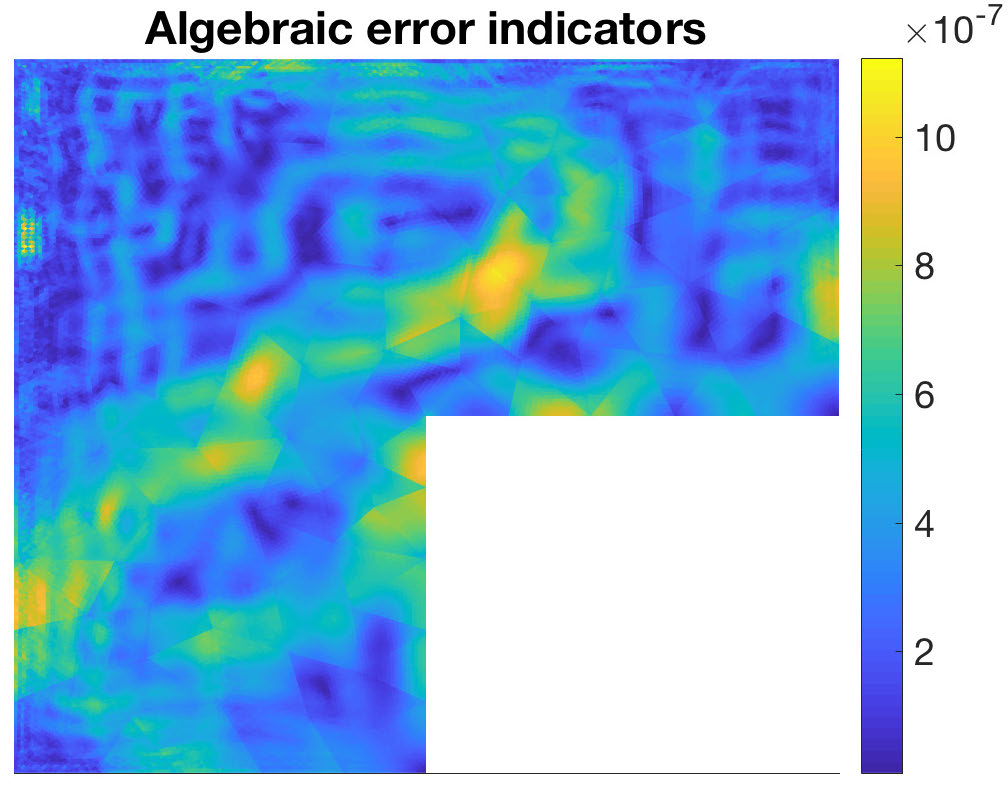
- estimating the local distribution of the errors over the computational domain;
- safe stopping criteria for iterative algebraic solvers: the algebraic error will lie below the discretization one;
- reliability and efficiency;
- recovering mass balance in any situation.
Details:
