Localization of the W^-1,q and distance norms

Distribution of the global (left) and local (right) p-Laplace residual lifting, p = 1.5

Distribution of the global (left) and local (right) p-Laplace residual lifting, p = 10

Effectivity index, transmission problem, left subdomain diffusion -0.01

Effectivity index, transmission problem, left left subdomain diffusion -0.33

Effectivity index, transmission problem, left left subdomain diffusion -0.99

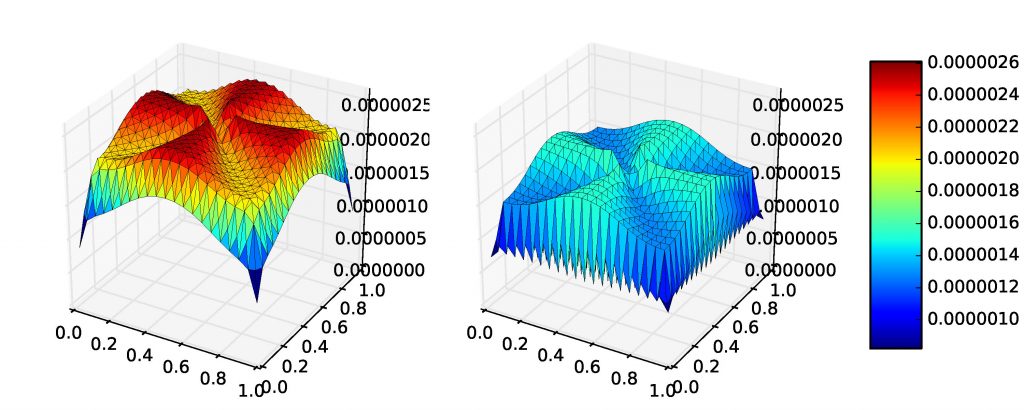
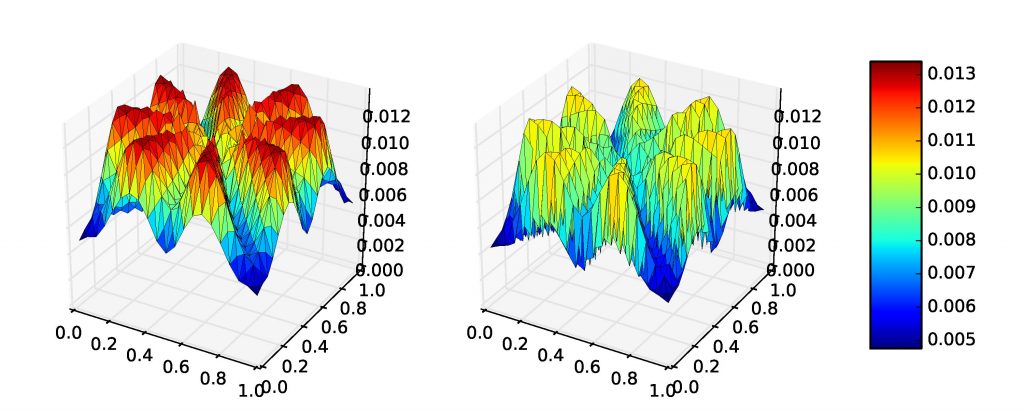
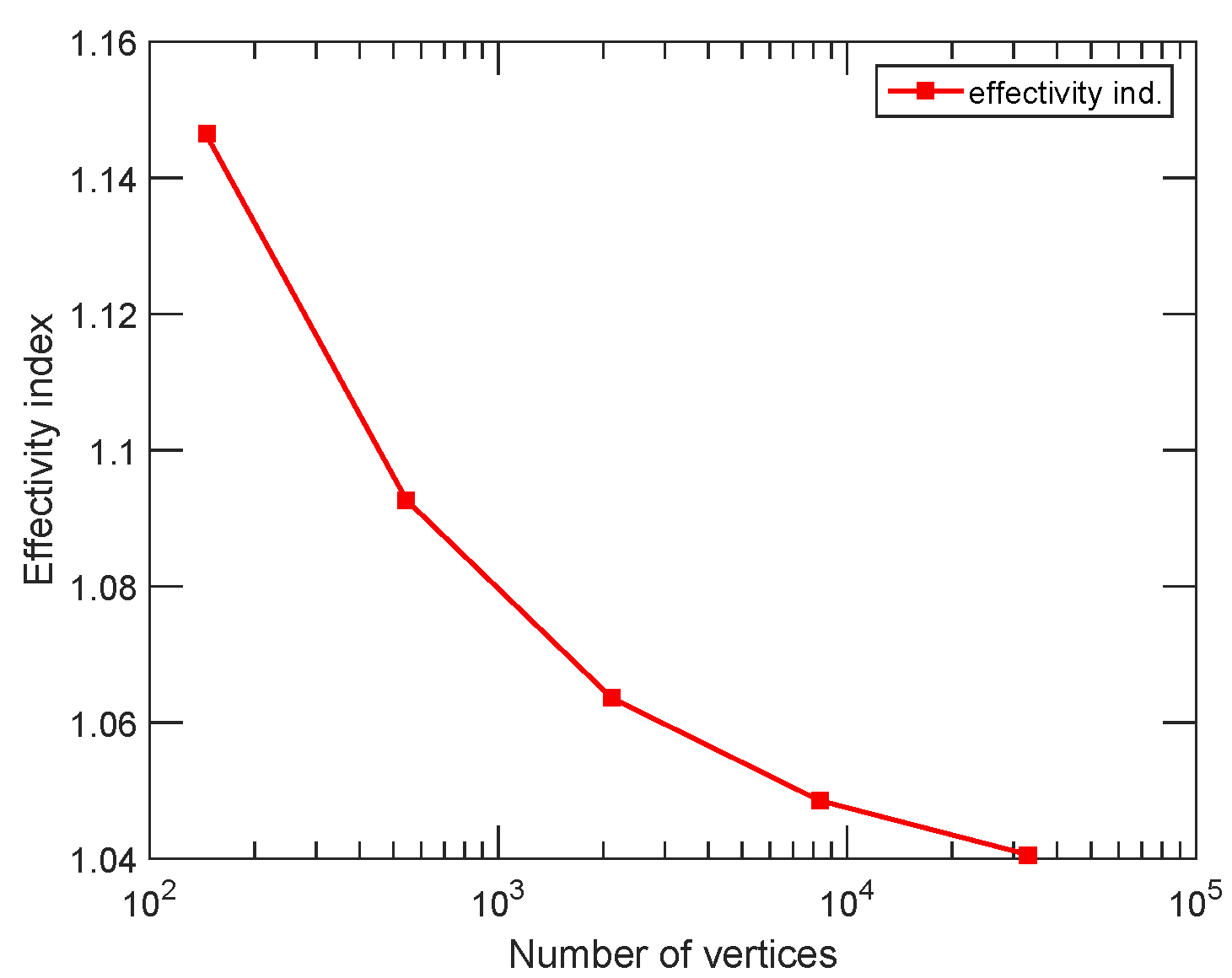
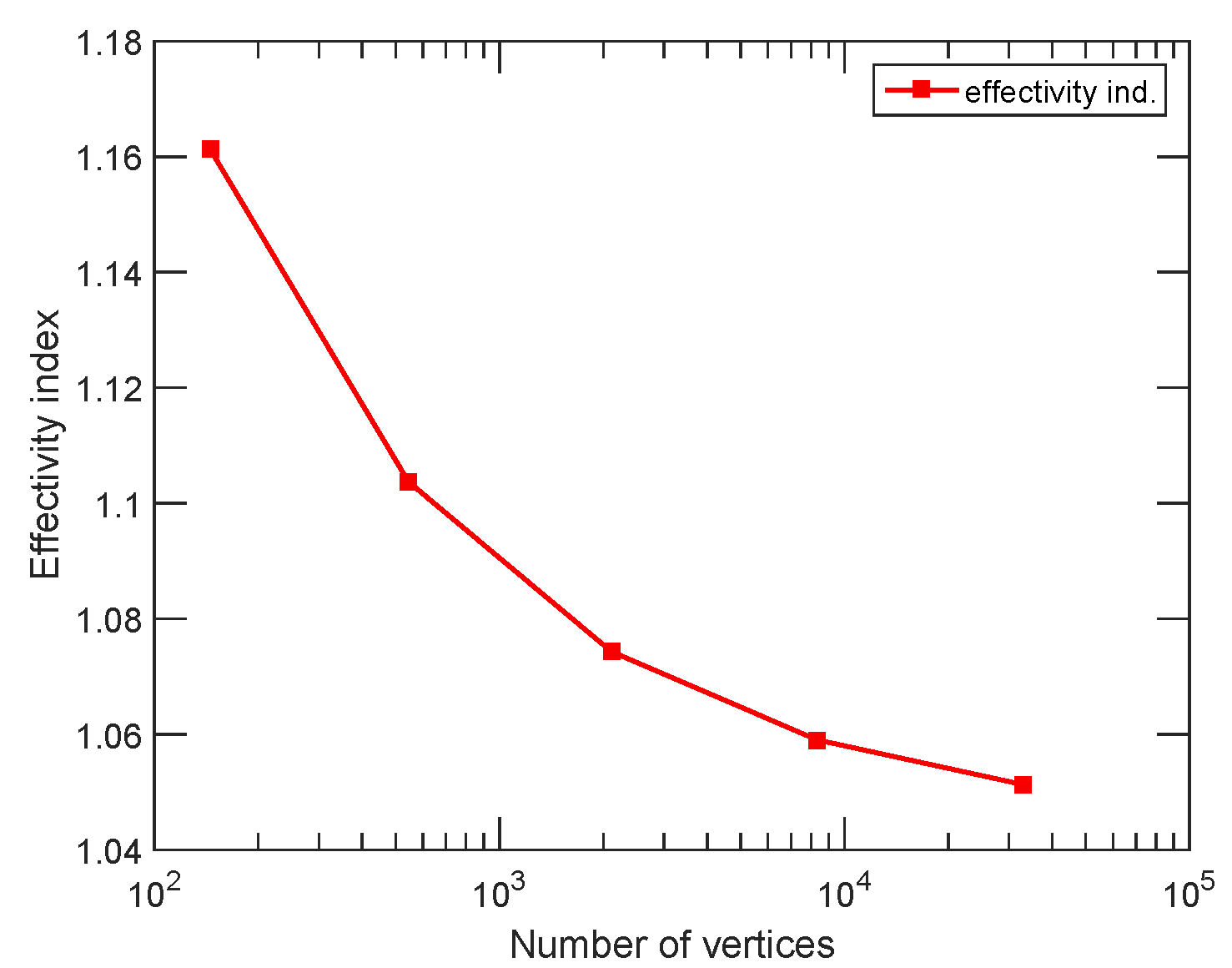
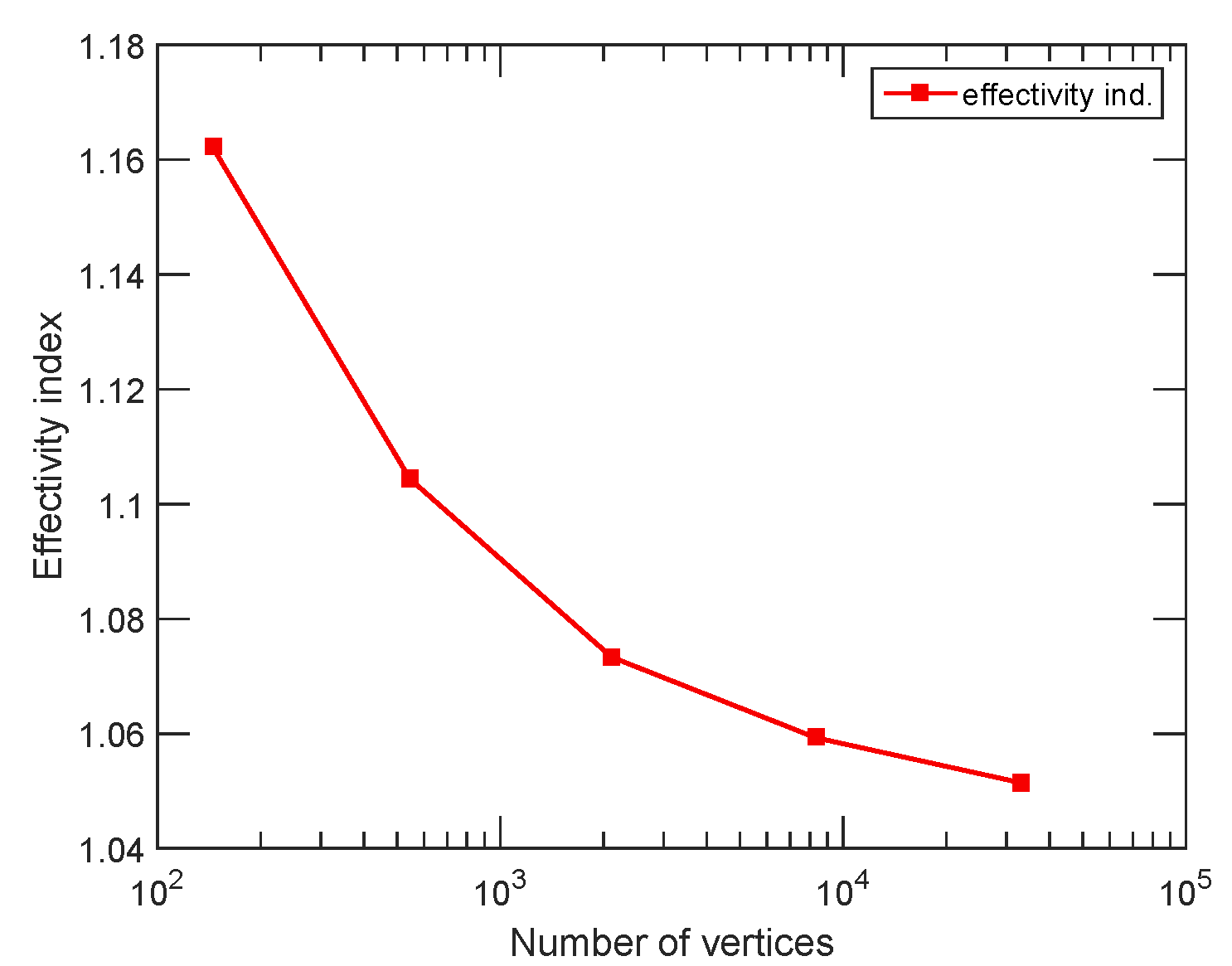
Main results:

• dual norm of any bounded linear functional on the Sobolev space W₀^1,p localizes under an orthogonality condition: equals the l^q sum of local contributions;
• estimates taking into account the violation of the orthogonality condition;
• distance to the Sobolev space H₀¹ localizes: equals the l² sum of local contributions (no orthogonality condition);
• implies local efficiency and robustness of a posteriori estimates for nonlinear and non-coercive partial differential equations in divergence form;
• includes the case of inexact solvers.

Details:

• H₀¹ setting including nonconformity: paper (preprint) with Patrick Ciarlet, Jr., presentation;
• W₀^1,p setting: paper (preprint) with Jan Blechta and Josef Málek, presentation.