Consider the following random walk problem. The secret is the initial location of the agent, encoded by a single natural number representing the distance from a given point, e.g. in meters. The distance is rounded up e.g. to a multiple of 50 to reduce the dependence to the initial position, then the agent takes a fixed number of steps. At each step the distance of the agent increases or decreases by 10 meters with the same probability. After this fixed number of random walk, the final location of the agent is revealed, and the attacker uses it to guess the initial location of the agent. The example is modeled by the following input program, available in the examples directory of HyLeak:
const MAX:=14;
secret int32 sec := [201,700];
observable int32 obs:= 0;
public int32 time := 0;
public int32 loc := 0;
public int32 seed := 0;
public int32 ran := 0;
if (sec <= 250) then
assign loc:=200;
elif (sec <= 350) then
assign loc:=300;
elif (sec <= 450) then
assign loc:=400;
elif (sec <= 550) then
assign loc:=500;
elif (sec <= 650) then
assign loc:=600;
elif (sec <= 750) then
assign loc:=700;
else
assign loc:=800;
fi
assign time:=0;
while (time < MAX) do
random ran := random(0,9);
if (ran < 5) then
assign loc:=loc+10;
else
assign loc:=loc-10;
fi
assign time:=time+1;
od
assign obs:=loc;
return;
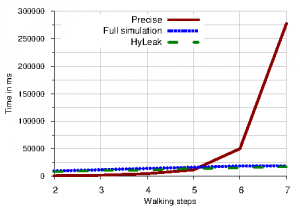
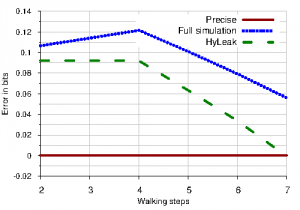
This problem is too complicated to analyze by precise analysis, because the analysis needs to explore every possible combination of random paths, amounting to an exponential number in the walking steps. It is also intractable to analyze with a fully statistical approach, since there are hundreds of possible secret values and the program has to be simulated many times for each of them to sufficiently observe the agent’s behavior.
However, the hybrid approach of HyLeak is effective to analyze the random walk problem, computing the leakage in significantly less time than the fully precise analysis and with significantly better precision than the fully statistical analysis. The following graphs compare HyLeak against a fully precise and a fully statistical approach on analysis time and error: