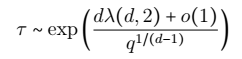Monday October 3
Ellen Saada : Invariant measures for multilane exclusion process
We consider the simple exclusion process on Zx{0,1}, that is, an “horizontal ladder” composed of 2 lanes. Particles can jump according to a lane-dependent translation-invariant nearest neighbour jump kernel, i.e. “horizontally” along each lane, and “vertically” along the scales of the ladder. We analyze the set of extremal invariant measures for this model. (Joint work with Gidi Amir, Christophe Bahadoran and Ofer Busani. ArXiv : 2105.12974)
Christophe Bahadoran : Invariant measures for asymmetric particle systems with a bottleneck
The totally asymmetric exclusion process (TASEP) with a slow bond, introduced by Janowski and Lebowitz (1992), can be seen as a model for traffic-flow with a bottleneck. Basu, Sarkar and Sly (2017) showed that for any subcritical slow bond rate, there exists a jammed steady state with a high density on the left and a low density on the right. Their approch uses the mapping between TASEP and last-passage percolation, that is not available for ASEP or more general models.
I will explain how to prove this using hydrodynamic limits and PDE theory, which also applies to models without an underlying percolation picture. In particular, a “non-crossing” condition appears on the current-density relation when the latter (unlike TASEP) exhibits a local minimum. (Work in progress)
Chiara Franceschini : Stochastic duality for asymmetric particle systems
In the context of Markov processes, stochastic duality is a powerful tool which allows to study a given process via another one, its dual. In this talk I will review the algebraic approach for stochastic duality, namely I will show how Lie algebras can be naturally associated to some interacting particle systems which can be symmetric, asymmetric and multi-species as well. Based on joint works with Gioia Carinci, Cristian Giardinà, Wolter Groenevelt, Jeffrey Kuan, Frank Redig and Zhengye Zhou.
Cristina Toninelli : Fredrickson-Andersen 2-spin facilitated model: sharp threshold
The Fredrickson-Andersen 2-spin facilitated model (FA-2f) on Z^d is a paradigmatic interacting particle system with kinetic constraints (KCM) featuring cooperative and glassy dynamics. For FA-2f vacancies facilitate motion: a particle can be created/killed on a site only if at least 2 of its nearest neighbors are empty. We will present sharp results for the first time, \tau, at which the origin is emptied for the stationary process when the density of empty sites (q) is small: in any dimension d ≥ 2 it holds
w.h.p., with λ(d,2) the threshold constant for the 2-neighbour bootstrap percolation on Z^d. This is the first sharp result for a critical KCM and settles various controversies accumulated in physics literature over the last four decades. We will explain the dominant relaxation mechanism leading to this result, give a flavour of the proof techniques, and discuss further results that can be obtained via our technique for more general KCM, including full universality results in two dimensions. [Joint work with I.Hartarsky and F.Martinelli]
Robert Jack : Examples of hydrodynamic behaviour in two-species exclusion processes
We discuss several different results for simple exclusion processes with two species of particles. We first show numerical results where inhomogeneous states appear in two-dimensional systems in which the species are driven in opposite directions, and we explain how these results can be rationalised by considering hydrodynamic PDEs for the density [1]. We then discuss how hydrodynamic equations in such models can be characterised, including a systematic analysis based on the method of matched asymptotics [2]. Finally, I will present some results [3] for large deviations in the hydrodynamic limit, associated with fluctuations of the entropy production in a simple model of active matter [4].
Assaf Shapira : Kinetically constrained lattice gases – cooperative vs. non-cooperative behavior
Kinetically constrained lattice gases is a family of models introduced in order to study glassy dynamics. They consist of particles hopping between the sites of a lattice and have a non-interacting equilibrium. However, kinetic constraints preventing them from moving may significantly slow down the dynamics. The extent to which the system slows down depends on the nature of the constraints, and in particular whether the model is non-cooperative, where an Arrhenius-type scaling is obsereved near criticallity, or cooperative, where a super-Arrhenius slowing down occurs. We will discuss these differences by considering two examples of kinetically constrained models, one non-cooperative introduced by Bertini and Toninelli, and the (cooperative) Kob-Andersen model.
♣♣♣
Tuesday October 4
Vivien Lecomte : Geometry of nonequilibrium interacting reaction networks
Building on Kirchhoff’s treatment of electrical circuits, Hill and Schnakenberg – among others – proposed a celebrated theory for the thermodynamics of Markov processes and linear biochemical networks that exploited tools from graph theory to build fundamental nonequilibrium observables. However, such simple geometrical interpretation does not carry through for arbitrary chemical reaction networks because reactions can be many-to-many and are thus represented by a hypergraph, rather than a graph. We propose a generalization of the geometric intuitions behind the Hill–Schnakenberg approach to arbitrary reaction networks. In particular, we give simple procedures to build bases of cycles (encoding stationary nonequilibrium behavior) and cocycles (encoding relaxation), that we interpret in terms of circulations and gradients. Such tools allow one to properly project nonequilibrium observables onto the relevant subspaces. We develop the theory for non-equilibrium reaction networks endowed with mass-action kinetics and enrich the description with insights from the corresponding stochastic models at the individual particle level.
Joint work with Sara Dal Cengio (Grenoble) and Matteo Polettini (Luxembourg)
Elisabeth Agoritsas : Dynamical mean-field theory of dense particle systems: global shear versus random local forcing
Disorder is ubiquitous in physical systems, and can radically alter their physical properties compared to their ‘pure’ counterparts. For instance, amorphous materials such as emulsions, foams, metallic glasses or biological tissues are all structurally disordered, and this has key implications for their rheological, mechanical or transport properties. Nevertheless, theoretical descriptions of such ‘driven’ amorphous materials remain challenging, despite of decades of extensive analytical and computational studies. The difficulties pertain to the interplay of competing sources of stochasticity, and to the resulting out-of-equilibrium nature of these systems. A standard model for amorphous materials, which allows to focus on the key role of their structural (positional) disorder, is provided by dense many-body systems of pairwise interacting particles. Here I will introduce an exact Dynamical Mean-Field Theory (DMFT) for these many-body systems, derived in the limit of infinite spatial dimension. In this framework, the many- body Langevin dynamics of the whole problem can be exactly reduced to a single scalar effective stochastic process, and dynamical observables such as pressure or shear stress can be computed for arbitrary driving protocols. Using this DMFT, we were in particular able to establish a direct equivalence between a global forcing (external shear) and a random local forcing (reminiscent of active matter), upon a simple rescaling of the control parameter (the accumulated strain). In this framework, global shear is thus simply a special case of a much broader family of local forcing, that can be explored by tuning its spatial correlations. Our predictions were moreover found to be in remarkably good agreement with two-dimensional numerical simulations. These results hint at a unifying framework for establishing rigorous analogies, at the mean-field level, between different families of driven disordered systems.
Pierre Le Doussal : Large deviations for diffusion in random media: crossover from the macroscopic fluctuation theory to the KPZ equation
I will first review the connections between diffusion in (time dependent) random media (DRM) and the KPZ equation. Then I will discuss our recent results on the large deviations for both problems and sketch how classical integrability allows to obtain the rate functions for (i) the KPZ equation using the weak noise theory (ii) the DRM as one example among the many diffusive systeme described by the macroscopic fluctuation theory (MFT). Finally I will sketch how the crossover occurs between the MFT and the WNT of the KPZ equation when the asymmetry is increased, which presumably extends to other models.
Alessandra Occelli : Hydrodynamics for the ABC model with slow/fast boundary
We consider the ABC model in contact with slow/fast reservoirs. It is an exclusion process with particles of type A,B and C that exchange positions in the discrete set of points {1,…, N-1} with a rate which is weakly asymmetric and depends on the type of particles involved in the exchange mechanism. At the boundary points x=1, N-1 particles can be injected or removed with rates depending on the type of particles involved. We prove that the hydrodynamic limit, in the diffusive time scale, is given by a system of nonlinear coupled equations with several boundary conditions depending on the strength of the reservoir’s action.
Clément Cosco : High moments of the 2D polymer partition function (joint work with Ofer Zeitouni)
We consider the model of directed polymers in dimension 1+2, in the temperature region where the partition function stays bounded in L2. In this regime, it is known that the diffusively rescaled log-partition function converges to a Gaussian log-correlated field. One natural question is to understand the behavior of the maximum of this rescaled field, which is related to the problem of understanding the probability distribution of the favorite point of the polymer trajectory. One major issue is that the field itself (before taking the limit) is not Gaussian, and one has to quantify how close it is to a Gaussian field. To do so, one has to compute high moments (going to infinity with the volume) of the partition function. I will present the sharp moment estimates that we obtained and discuss the background and open questions.
Aurélien Grabsch : A Closed Equation for Correlation Profiles in Single-File Systems
Single-file transport, where particles diffuse in narrow channels while not overtaking each other, is a fundamental model for the tracer subdiffusion observed in confined systems, such as zeolites or carbon nanotubes. This anomalous behavior originates from strong bath-tracer correlations in 1D, which we characterise in this talk through Generalised Density Profiles (GDPs). These GDPs have however remained elusive, because they involve an infinite hierarchy of equations. Here, for the Symmetric Exclusion Process, a paradigmatic model of single-file diffusion, we break the hierarchy and unveil a closed equation satisfied by these correlations, which we solve. Beyond quantifying the correlations, the central role of this equation as a novel tool for interacting particle systems will be further demonstrated by showing that it applies to out-of equilibrium situations, other observables and other representative single-file systems. REFS:
- Generalized Correlation Profiles in Single-File Systems. Alexis Poncet, Aurélien Grabsch, Pierre Illien, Olivier Bénichou. Phys. Rev. Lett. 127, 220601 (2021), arXiv:2103.13083
- Closing and Solving the Hierarchy for Large Deviations and Spatial Correlations in Single-File Diffusion. Aurélien Grabsch, Alexis Poncet, Pierre Rizkallah, Pierre Illien, Olivier Bénichou
Kirone Mallick : Exact solution of the macroscopic fluctuation theory for symmetric exclusion
Interacting diffusive particle systems are considered as paradigms for non-equilibrium statistical physics. Their macroscopic behaviour follows a variational principle, proposed by G. Jona-Lasinio and his collaborators, known as the Macroscopic Fluctuation Theory (MFT), in which fluctuations far from equilibrium are determined at a coarse-grained scale by two coupled non-linear hydrodynamic equations. In this talk, we shall show that, for the exclusion process, the MFT equations are classically integrable and can be solved with the help of the inverse scattering method, originally used to study solitons in the KdV or the NLS equations. This exact solution will allow us to calculate the large deviations of the current and the optimal profiles that generates a given fluctuation, both at initial and final times.
♣♣♣
Wednesday October 5
Paul Chleboun : Mixing times for Facilitated Exclusion Processes.
We consider facilitated exclusion processes (FEP) in one dimension. These models belong to a class of kinetically constrained lattice gases originally motivated by glassy systems. Under the dynamics a particle can move to a neighbouring site provided that the target site is empty (the exclusion rule) and the other neighbour of the departure site is occupied (the constraint). These processes have recently attracted attention due to their absorbing state phase transition and interesting hydrodynamic limit behaviour. We examine the mixing time, the time to reach equilibrium, on an interval with closed boundaries and also with periodic boundary conditions. On the interval we observe that asymmetry significantly changes the mixing behaviour. The analysis naturally splits into examining the time to reach the ergodic configurations (irreducible component) followed by the time needed to mix on this set of configurations. This is ongoing work with James Ayre (Oxford).
Laure Marêché : Universality for Bootstrap Percolation and Kinetically Constrained Models
Bootstrap percolation and kinetically constrained models are two classes of statistical mechanics models that share several characteristics: they are models on graphs in which each vertex of the graph can be in state 0 or 1, and can change state only when a constraint of the form “there are enough zeroes around the vertex” is satisfied. In both classes of models, the behavior of the system depends sharply on the choice of the constraint, and there is an infinite number of possible constraints. Therefore a very important question is that of universality: can this infinity of models be sorted into a finite number of classes according to their behavior? We will present answers for both bootstrap percolation and kinetically constrained models, highlighting the similarities and the differences between the two.
Ivailo Hartarsky : Bootstrap percolation and cellular automata with death
We consider two classes of models. The first one is bootstrap percolation. The second one is attractive cellular automata with death. For instance, one may think of oriented percolation, i.e. the discrete time synchronous contact process. It turns out that these two classes are equivalent in a very strong sense, entailing interesting consequences in both directions. In particular, we will discuss results related to the non-triviality of their phase transition and the sharpness of this transition. Based on https://arxiv.org/abs/2203.16366 joint with R. Szabó, and https://arxiv.org/abs/2112.01778
Grégory Schehr : First-passage properties of persistent random walks/run-and-tumble particles
Persistent random walks, introduced in the maths literature by M. Kac, have become popular models of active matter where they are known under the name of run-and-tumble particles (RTP). In its simplest version, an RTP in dimension d, performs a ballistic motion along a certain direction, chosen uniformly at random, at a constant speed v_0 (“run” ) during a certain exponential random “time of flight” \tau. Following this run, it “tumbles”, i.e., chooses a new direction uniformly at random and then performs a new run along this direction with speed v_0 during an exponential random time, and so on. I will present exact results for two first-passage problems related to RTPs: (i) the probability that the x-component of a single RTP in d-dimension has not changed sign up to time t and (ii) the probability that two independent RTPs on the line do not cross up to time t.
Amic Frouvelle
We consider models of active particles moving at constant speed and having a body orientation represented by a rotation matrix. Particles align with their neighbors and are subject to angular noise, either continuously or by jump processes. In the mean-field limit, we obtain a kinetic model for the evolution of the probability density of particles at a given position and given body orientation. By describing the local equilibria, we can perform hydrodynamic scaling for which the formal limit is given by a first-order equation of evolution of the local density and local body orientation. The study of this macroscopic model is challenging, we will present results of hyperbolicity, as well as ideas to tackle the fact that it is by nature non-conservative. This is based on joint works with Pierre Degond (Toulouse), Antoine Diez (Kyoto), Sara Merino-Aceituno (Vienna) and Ariane Trescases (Toulouse).