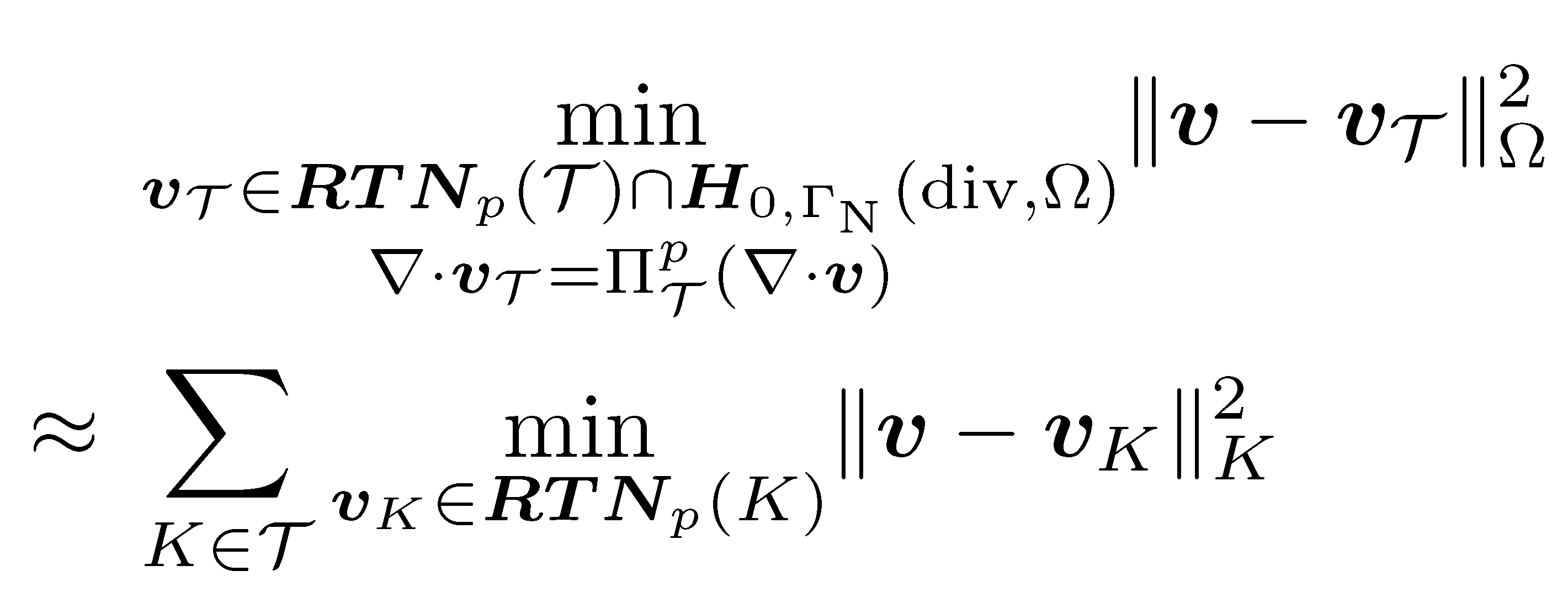 For any H(div) function v with zero normal flux over part of the boundary and piecewise polynomial divergence |
Main results:
- global-best approximation (constraints on normal component continuity and divergence) is equivalent to the sum of independent local-best approximations (no constraints);
- gives rise to a simple stable local commuting projector in H(div);
- this projector delivers approximation error equivalent to the local-best approximation;
- leads to optimal hp approximation estimates in H(div);
- applies under the minimal necessary Sobolev regularity;
- gives optimal a priori hp-error estimates for mixed and least-squares finite element methods.
Details:
- paper (preprint) with Alexandre Ern, Thirupathi Gudi, and Iain Smears, see also presentation;
- local- and global-best equivalence in H(curl): paper (preprint) with Théophile Chaumont-Frelet.
