p-robust multilevel algebraic error estimator & solver

Comparative performance (number of iterations and elapsed time) of the a-posteriori-steered p-robust multilevel solvers

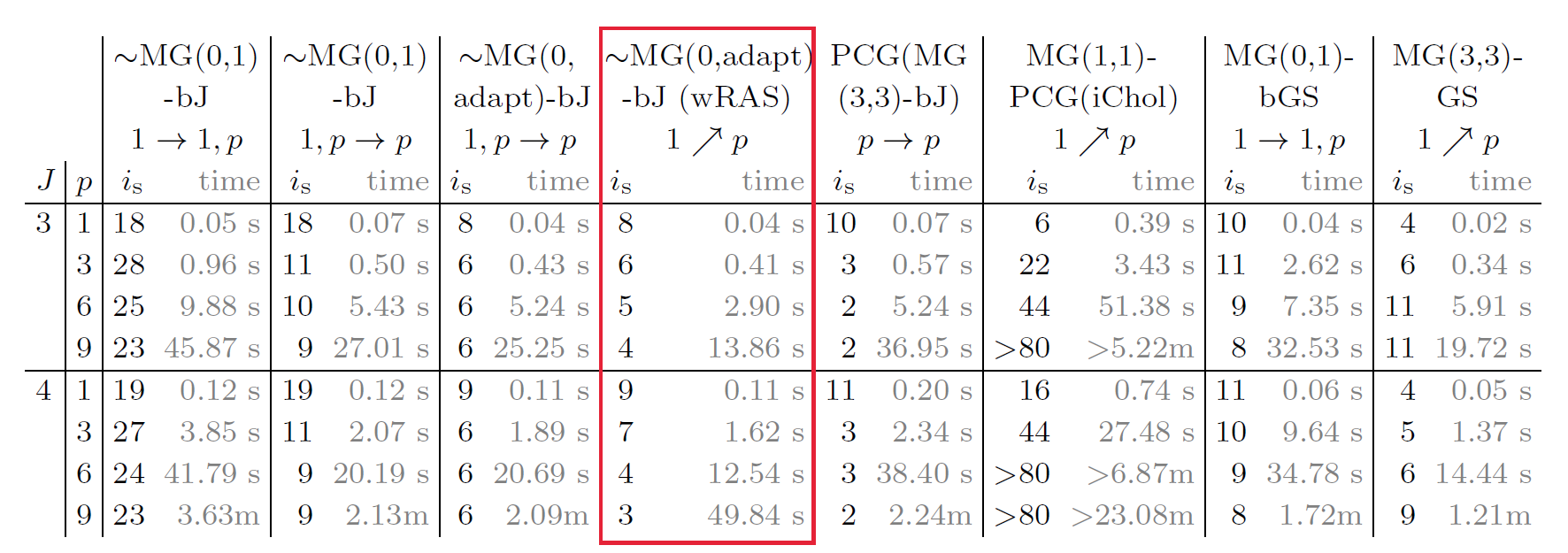
Main results:

• multilevel a posteriori estimator of the algebraic error;
• guaranteed (reliable) and efficient:
  ,
  ;
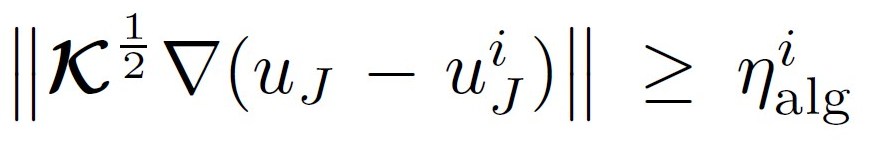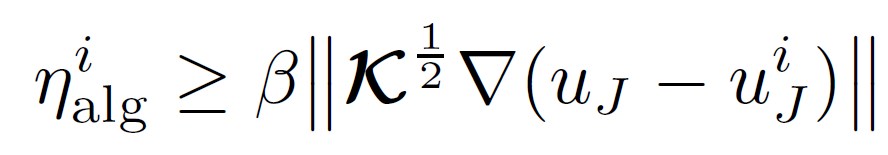• polynomial-degree robust: β independent of p;
• gives rise to a multilevel iterative algebraic solver with contraction independent of the polynomial degree p:
  ;
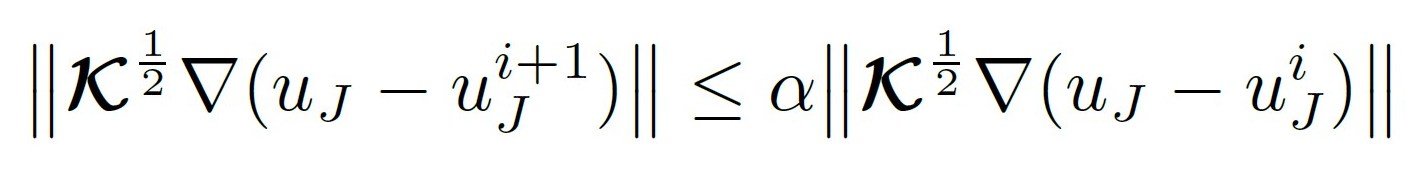• equivalence estimator – solver: α = √ (1 – β²);
• adaptive number of smoothing steps / adaptive smoothing possible.

Construction:

• global coarsest-level solve of lowest-order (p=1);
• local patchwise contributions from other levels;
• corresponds to V-cycle geometric multigrid with zero pre– and one (or adaptive number of) post-smoothing steps by block-Jacobi;
• optimal step size for the descent direction.

Details in Ph.D. thesis of Ani Miraçi, Ph.D. defense presentation; with Jan Papež:

• basic theory: paper;
• adaptive number of smoothing steps: paper;
• adaptive smoothing: paper (preprint).