 Estimated error (left) and actual error (right), L-shaped 3D domain, top view, broken patchwise equilibration |
 Estimated error (left) and actual error (right), L-shaped 3D domain, top view (top) and side view (bottom), patchwise equilibration |
Main results:
- H(curl)-stable polynomial extension on a tetrahedron;
- stable broken H(curl) polynomial extension on a patch of thetrahedra;
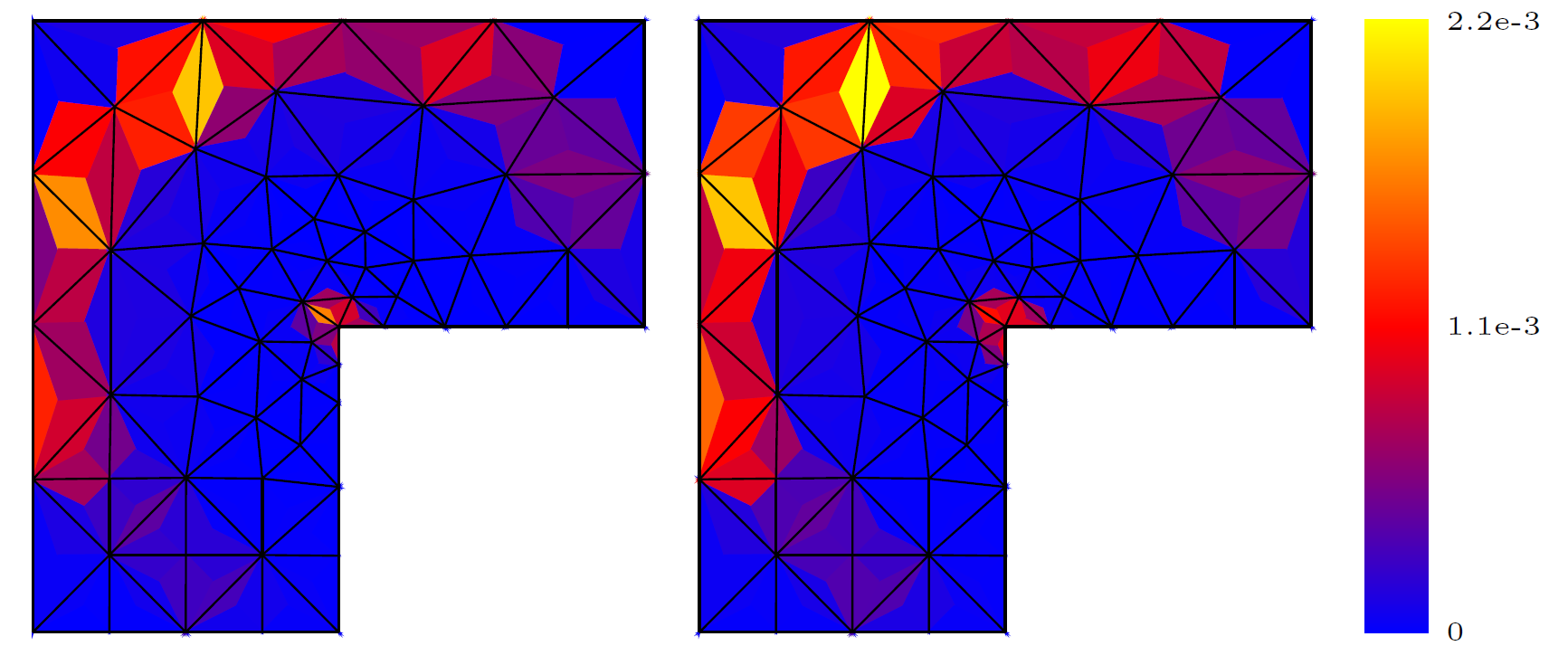
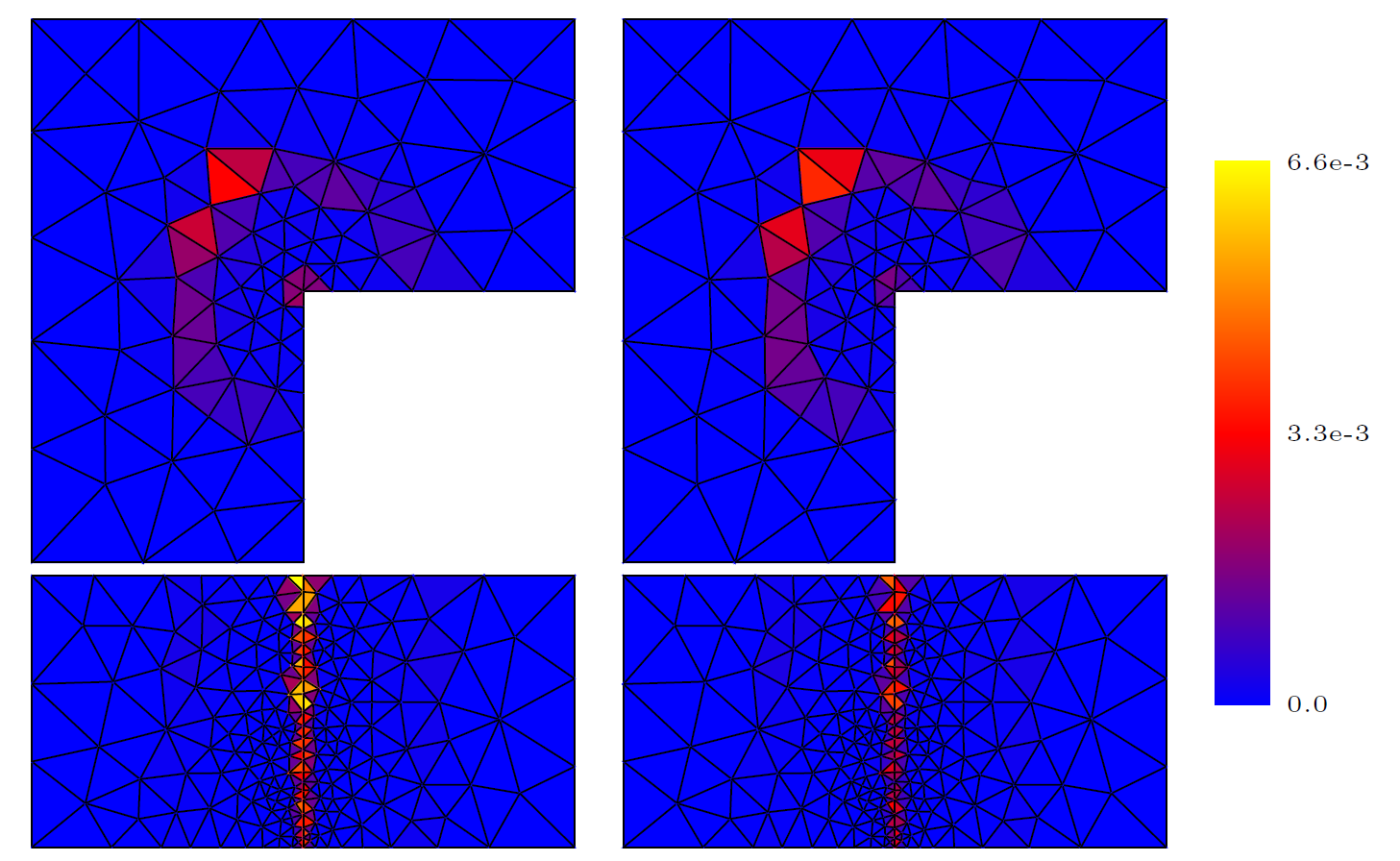
- a posteriori error estimates of H(curl)-conforming methods: reliable (guaranteed), locally efficient, polynomial-degree-robust, and inexpensive.
Details:
- H(curl)-stable polynomial extension on a tetrahedron: paper (preprint) with Alexandre Ern and Théophile Chaumont-Frelet;
- stable broken polynomial extension and broken patchwise equilibration: paper (preprint) with Alexandre Ern and Théophile Chaumont-Frelet;
- patchwise equilibration: preprint with Théophile Chaumont-Frelet;
- presentation.
