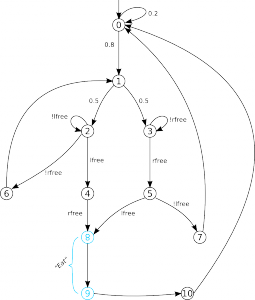Introduction
To test the model-checking performance of PLASMA we created increasingly complex models based on the probabilistic dining philosophers of (Pnueli, Zuck 1986). Especially we used this range of model for our IGRIDA distributed experimentation. Results of this experimentation can be found here. Here is the model for the case of 3 philosophers. You can download a Plasma Lab project file containing models and a liveness property for 3 philosophers to 300 philosophers.
Model
Important!
// Randomised dining philosophers based on (Pnueli, Zuck 1986)
dtmc
formula lfree = p2>=0 & p2<=4 | p2=6 | p2=10; formula rfree = p3>=0 & p3<=3 | p3=5 | p3=7; module phil1 p1: [0..10]; [] p1=0 -> 0.2 : (p1’=0) + 0.8 : (p1’=1);
[] p1=1 -> 0.5 : (p1’=2) + 0.5 : (p1’=3);
[] p1=2 & lfree -> (p1’=4);
[] p1=2 & !lfree -> (p1’=2);
[] p1=3 & rfree -> (p1’=5);
[] p1=3 & !rfree -> (p1’=3);
[] p1=4 & rfree -> (p1’=8);
[] p1=4 & !rfree -> (p1’=6);
[] p1=5 & lfree -> (p1’=8);
[] p1=5 & !lfree -> (p1’=7);
[] p1=6 -> (p1’=1);
[] p1=7 -> (p1’=1);
[] p1=8 -> (p1’=9);
[] p1=9 -> (p1’=10);
[] p1=10 -> (p1’=0);
endmodule
module phil2 = phil1 [p1=p2, p2=p3, p3=p1] endmodule
module phil3 = phil1 [p1=p3, p2=p1, p3=p2] endmodule
// labels
label “hungry” = ((p1>0)&(p1<8))|((p2>0)&(p2<8))|((p3>0)&(p3<8)); label “eat” = ((p1>=8)&(p1<=9))|((p2>=8)&(p2<=9))|((p3>=8)&(p3<=9));
We checked a property saying “fatally one of the philosophers will be hungry and after that, fatally, one of the philosophers will eat”.
Important!
F<=#1000 (hungry &(X<=#1 F<=#1000 eat))We checked this property with the Chernoff method and parameters epsilon = 0.001, delta = 0.01. With these parameters Plasma Lab will check the property with a confidence of 99% and a precision of 0.1%.
We used this model to benchmark Plasma Lab and compare it against others Statistical Model Checking tools. The results are given below.
| #Philosophers | Time (s) |
|---|---|
| 3 | 6.27 |
| 10 | 16.629 |
| 30 | 89.100 |
| 100 | 724.944 |
| 300 | 4347.504 |
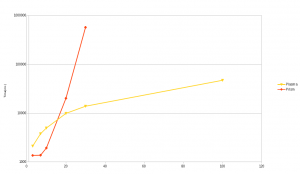
Comparison between PRISM Numerical Analysis and Plasma Lab. Time(ms) against number of philosophers.
Importance splitting
We experiment the importance splitting algorithm on this example. We consider the model with 150 philosophers and we estimate the probability that a given philosopher will eat within 30 steps. This property \(\phi=F^{30} Eat\) can be decomposed into 5 sub-properties that the philosopher must satisfy before satisfying \(\phi\):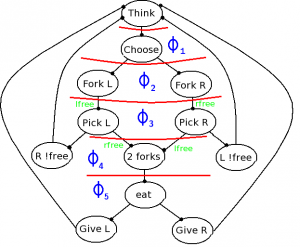
- \(\phi_0=F^{30} Think\)
- \(\phi_1=F^{30} Choose\)
- \(\phi_2=F^{30} Try\)
- \(\phi_3=F^{30} 1^{st} Stick\)
- \(\phi_4=F^{30} 2^{nd} Stick\)
- \(\phi_5=F^{30} Eat\)
We first consider the following observer to compute a score function for this model:
Important!
observer rareObserver
score : double init 0;
c : clock;
decided : bool init false;
s : [0..5] init 0;
[] p1=1 & s=0 -> (score’=1)&(s’=1);
[] (p1=2 | p1=3) & (s=1) -> (score’=2)&(s’=2);
[] (p1=4 | p1=5) & (s=2) -> (score’=3)&(s’=3);
[] p1=8 & (s=3) -> (score’=4)&(s’=4);
[] p1 >8 & score <5 & (s=4) -> (score’=5)&(s’=5);
[] (c=30) -> (decided’=true);
endobserver
This score function increase the score each time a new sub-property is satisfied. It is adequate to be used with the fixed level algorithm.
We then refine the observer such that the score also takes into account the time at which a new level is satisfied (using the clock c). It is such that the score is between \(]0,1[ \text{ if } \phi_1\) is satisfied, between \(]1,2[ \text{ if } \phi_2\) is satisfied, etc… When the score becomes higher than 4 the property \(\phi\) is satisfied. This observer is optimized for the adaptive algorithm.
Important!
observer rareObserver
decided : bool init false;
c : clock;
s : [0..5] init 0;
[] c=30 -> (decided’= true);
[] p1=1 & s=0 -> (s’=1);
[] (p1=2 | p1=3) & (s=1) -> (s’=2);
[] (p1=4 | p1=5) & (s=2) -> (s’=3);
[] p1=8 & (s=3) -> (s’=4);
[] p1 >8 & (s=4) -> (s’=5);
endobserver
observer score
score : double init 0;
[] true -> (score’=s-(s-c)/(s-31));
endobserver
The model with the observer can be downloaded here.