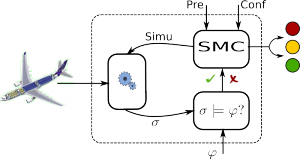
Statistical Model Checking

Model Checking (MC) [BK08,CGP99] is a widely recognized approach to guarantee correctness of a system. The technique relies on algorithms that check whether all executions of a system satisfy some properties stated in a specification logic. If this is the case, then the system is correct, else a bug is reported. Contrary to testing, MC is thus capable of detecting all bugs of a system. This comes with the price that MC is generally slower. First implementations of model checking suffered from so-called state space explosion problems and could only be applied to small academic models. New techniques build on symbolic data structures and/or heuristics that make them capable of analyzing large-size systems that are part of our daily life.  MC, for which Clarke, Sifakis and Emerson received the ACM Turing award in 2007, has been implemented in several powerful tools [SPIN,SMV] that are successfully used in industry.  Classical model checking techniques are Boolean (either the system satisfies a property or it does not). Unfortunately such a view is extremely sensitive to changes made in the design and is not able to quantify their impacts (both minor and major changes may reverse the verification outcome).  This view is now obsolete: the designers need a finer analysis that allows to quantify the impacts of any change in the design. This has motivated the development of a series of new techniques (under the name of Probabilistic Model Checking) and tools [PRISM,BK08] capable of quantifying the likelihood for a system (whose behaviors naturally depend on stochastic information) to satisfy some property.  Adding explicitly rich features (e.g., real time) in specifications is also needed. Indeed, in many situations it is not enough to know whether something will or will not happen; rather, one needs to have a precise estimate of the time when some situation will arise. This motivated the creation of a number of new techniques under the name of timed model checking. First timed MC techniques were again Boolean. The UPPAAL [UPPAAL] tool set implemented in Aalborg and Uppsala is the leader in the domain.  New techniques, also implemented in UPPAAL and PRISM permit to reason quantitatively on timed systems.The problem with MC-based approaches is that even though heuristics exist (partial order, symbolic approach, BDDs, etc.), they still suffer from the state-space explosion problem. This is especially the case when the system is obtained as the combination of several subsystems. Moreover, when moving to rich systems such as those with real time features, most of the model checking problems become undecidable.

To overcome the above difficulties we propose to work with Statistical Model Checking [KZHHJ09,You05,You06,SVA04,SVA05,SVA05b] an approach that has recently been proposed as an alternative to avoid an exhaustive exploration of the state-space of the model. The core idea of the approach is to conduct some simulations of the system, monitor them, and then use results from the statistic area (including sequential hypothesis testing or Monte Carlo simulation) in order to decide whether the system satisfies the property or not with some degree of confidence. By nature, SMC is a compromise between testing and classical model checking techniques. Simulation-based methods are known to be far less memory and time intensive than exhaustive ones, and are oftentimes the only option. SMC has been implemented in a series of tools that have defeated PRISM on several case studies. Unlike more “academic” exhaustive techniques, SMC gets widely accepted in various research areas such as systems biology [CFLHJL08,JCLLPZ09,PRISM] or software engineering [CDL10], in particular for industrial applications [BBBCDL10,BBDLS10]. There are several reasons for this success. First, it is very simple to implement, understand and use (especially by industry, software engineers, and generally all people that are not pure researchers but customers for our results and tools). Second, it does not require extra modeling or specification effort, but simply an operational model of the system that can be simulated and checked against state-based properties. Third, it allows to model check properties that cannot be expressed in classical temporal logics ([CDL10] contains an example where the property is the comparison of two Fourier transforms for Simulink [SIMULINK]).

We briefly recap statistical algorithms permitting to answer the following two types of questions :

1. Qualitative : Is the probability for a given NPTAto satisfy a propertygreater or equal to a certain threshold?
2. Quantitative : What is the probability forto satisfy Each run of the system is encoded as a Bernoulli random variable that is true if the run satisfies the property and false otherwise.

Qualitative Question

This problem reduces to test the hypothesis against . To bound the probability of making errors, we use strength parameters andand we test the hypothesis andwithandThe intervaldefines an indifference region, andandare used as thresholds in the algorithm. The parameteris the probability of accepting whenholds (false positives) and the parameter is the probability of acceptingwhenholds (false negatives). The above test can be solved by using Wald’s sequential hypothesis testing [Wald45].
This test computes a proportionamong those runs that satisfy the property. With probability 1, the value of the proportion will eventually crossor and one of the two hypothesis will be selected.

Quantitative Question

This algorithm [You06] computes the number of runs needed in order to produce an approximation interval for with a confidence The values of and are chosen by the user and relies on the Chernoff-Hoeffding bound.