In the railway domain, an interlocking is the system ensuring safe train traffic inside a station by controlling its active elements such as the signals or points. Modern interlockings are configured using particular data, called application data, reflecting the track layout and defining the actions that the interlocking can take. The safety of the train traffic relies thereby on application data correctness, errors inside them can cause safety issues such as derailments or collisions. Given the high level of safety required by such a system, its verification is
a critical concern. In addition to the safety, an interlocking must also ensure that availability properties, stating that no train would be stopped forever in a station, are satisfied.
We have analyzed with Plasma Lab a train interlocking case-study, in collaboration with Université Catholique
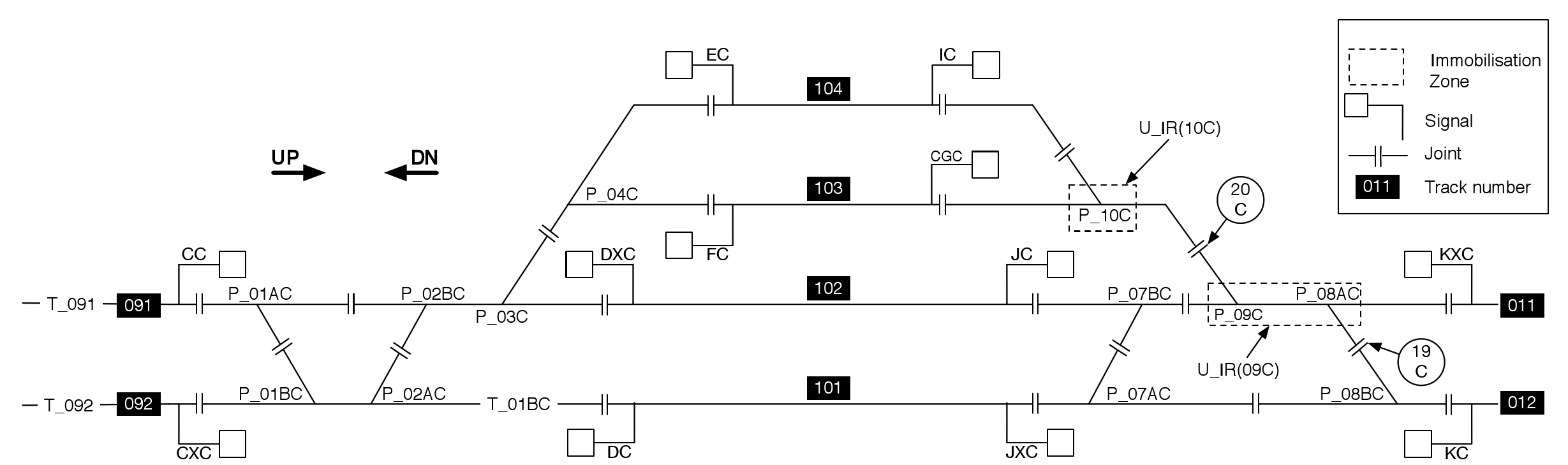
de Louvain and Alstom. We have considered the layout of the Braine l’Alleud station’s interlocking system, a medium size railway station of the Belgian network, shown in Fig. 1 below.
Each station is composed of a set of physical components:
– The points (e.g. P_01BC) are the track components that guide the train from one track to another.
– The signals (e.g CC) are the interface between the interlocking and the trains.
– The track segments (e.g T_01BC) are the tracks where a train can be detected. They can be either occupied by a train or clear. On a station they are delimited each other by the joints.
A route is the path that a train must follow inside a station. A route is named according to its origin and destination point. For instance, Route R_CC_102 starts from Signal_CC and ends on Track_102. A route can be set if it is reserved for a train or unset on the contrary. When a train is approaching to a station, a signalman will perform a route request to the interlocking in order to ask if the route can be set. The interlocking will handle this request and will accept or reject it according to the station state. To do so, an interlocking uses logical components like the subroutes or the immobilization zones, materializing the availability of some physical components. Such components are locked or released if they are not requested. Braine l’Alleud station is controlled by a unique interlocking composed of 32 routes, 12 signals, 13 track-circuits, and 12 points.
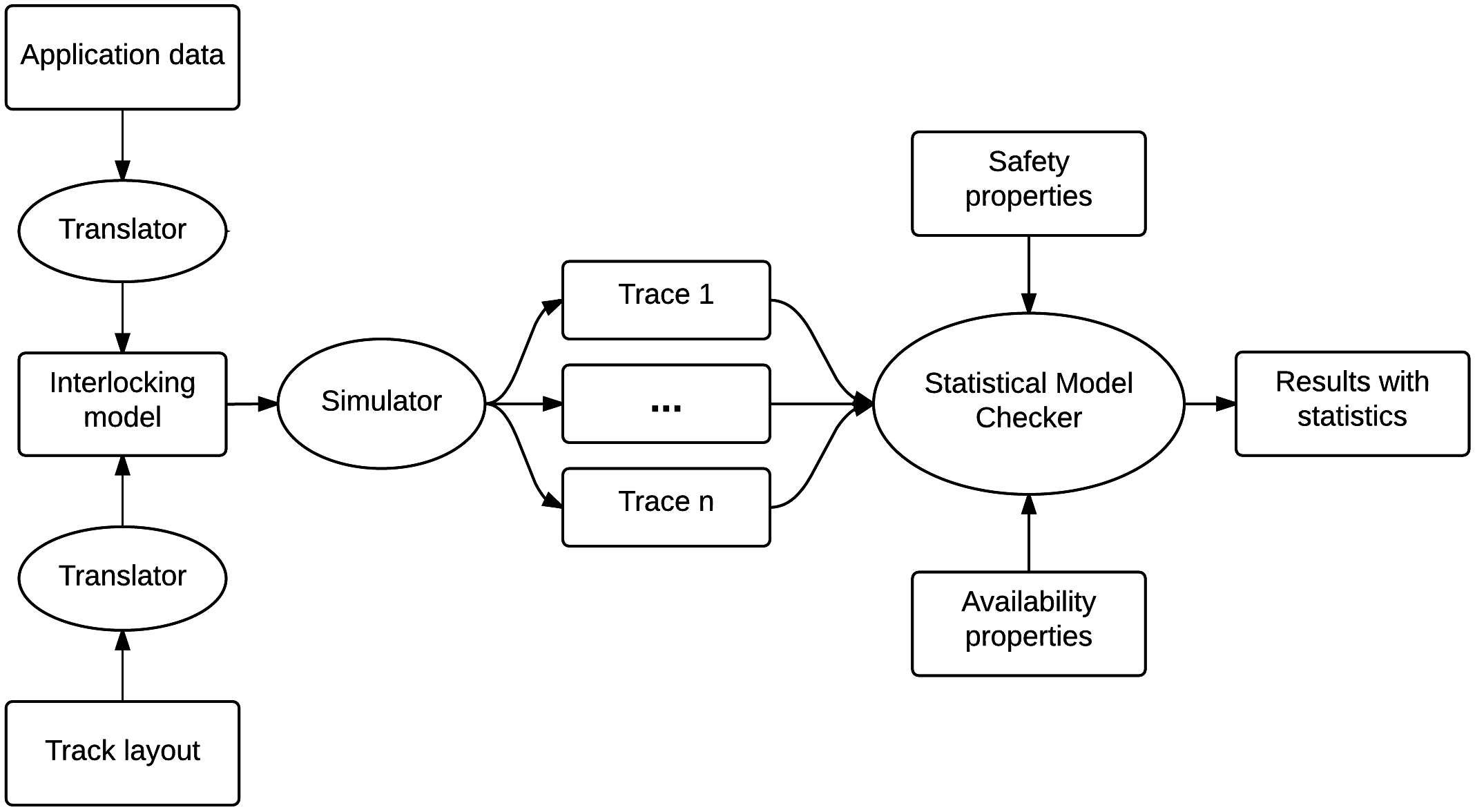
We verify two types of requirements: safety properties (e.g., avoid collisions of two trains on the same track), and availability properties (e.g., a route can always be eventually set). The verification process that we apply is described on Fig. 2. We use a simulator developed by Université Catholique de Louvain that is able to generate traces of the interlocking systems from a track layout and application data. This simulator is plug with Plasma Lab using a small interface developed with Plasma Lab’s API. Then, the traces generated by the simulator are be used by Plasma Lab SMC algorithms to measure the correctness of the system. We have used Monte-Carlo and importance splitting algorithms to verify this system.
Experiments
We evaluate the validity of our approach through experimental results. Indeed, now that we have a model and a verification process, we need to ensure that it will efficiently detect the errors leading to safety or availability issues. For the first experiment, we introduced several errors in the application data in order to test if they will be detected through simulations:
- a. Missing condition for moving a point in a route request.
- b. Point moved to a wrong position when setting a route.
- c. Subroute not properly locked when setting a route.
- d. Condition missing for releasing a subroute.
- e. Condition missing for releasing an immobilisation zone.
- f. Irrelevant additional conditions for releasing a component.
We consider 5 BLTL properties, and we analyze with Monte Carlo and 100 simulations the probability that the property is satisfied according to the type of error that has been introduced in the model. A non-zero probability means that a safety or availability issue occurred on at least one simulation. In this case, we have then the certainty that the interlocking is not correct. As we can see on Table 1, each error introduced in the application causes the violation of at least one requirement, which means that all the errors have been detected through 100 simulations of one day. Using these results, it is possible to analyse which issues are caused by specific errors. For instance, injecting an error of type f. only causes availability issues.
| Type of error | Safety requirements | Availability requirements | Time (sec.) | |||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | ||
| a. | 0 | 100 | 0 | 0 | 0 | 1424 |
| b. | 0 | 0 | 100 | 100 | 98 | 1086 |
| c. | 91 | 69 | 29 | 63 | 100 | 1348 |
| d. | 93 | 100 | 0 | 33 | 99 | 1845 |
| e. | 72 | 97 | 0 | 79 | 100 | 1199 |
| f. | 0 | 0 | 0 | 100 | 100 | 1652 |
Table 1: Execution time (in seconds) and probability (in percent) of detecting an issue violating a BLTL requirement (from 1 to 5) when errors are inserted (from a. to f.) on Braine l’Alleud application data.
Importance splitting for collision detection
The second experiment deals with the safety requirement stating that no collision can occur in the station. The no collision requirement can easily be split in different levels. The first level is reached when two conflictual routes are set together in the station. Two routes are conflictual if they share at least one common track segment. For instance, R_CXC_102 and R_DXC_091 in Fig. 1 are conflictual. The next level is reached when there is only one track segment between two trains following conflictual routes if and only if no train is beyond the track segment where the collision can occur. According to the previous example, if the train following Route R_CXC_102 is on Track segment T_01BC and the train following Route R_DXC_091 on Track_102, there is only a difference of one track segment. The third level is the event that we want to detect: the collision.
Table 2 presents statistics for simulations of 1 day with an error of type d. on the application data. Confidence intervals are obtained using a normal distribution. The number of experiments and the number of simulations per experiment are chosen in order to have the same total number of simulations for Monte Carlo and importance splitting (1000 in that case). As we can see, even for a medium size station such as Braine l’Alleud where errors are rapidly detected with Monte Carlo, importance splitting can give similar results much faster for a same number of simulations.
| Statistics | Monte Carlo | Importance splitting |
|---|---|---|
| # experiments | 10 | 1 |
| # simulations per experiment | 100 | 1000 |
| Average execution time (sec) | 257 | 1320 |
| Average arithmetic mean (%) | 93.9 | 93.94 |
| Standard deviation (%) | 1.21 | 0.75 |
| 99.9%-confidence interval (%) | [92:71; 95:12] | [91:43; 96:45] |
Table 2: Comparison between Monte Carlo and importance splitting algorithms for collision detection when an error of type f. is introduced on Braine l’Alleud application data