We consider a network of processes organized in a ring. Tokens can be assigned to each process. The network is said to be stable if only one process is “privileged” with a token, otherwise the network is unstable. A self-stabilisation algorithm allows the network to automatically returns to a stable configuration within a finite number of steps. We study the protocol proposed by Israeli and Jalfon, also described here. The model implemented in PLASMA is available here.
We first compute the minimum probability, over all the initial configurations, that the network returns in a stable configuration within a given number of steps. We plot below the results obtained for 2 models, one within 15 processes, and one with 20 processes. The red lines depict the results obtained with our smart hypothesis testing algorithm, while the black lines are the exact results computed with PRISM model checker. The results show that our algorithm correctly estimate the probability when the time bound and the probability are either large or small, but that we only compute an under-approximation for medium time bound. The error becomes wider when the model complexity increase from 15 to 20 processes.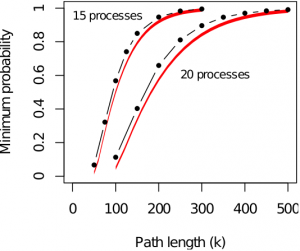
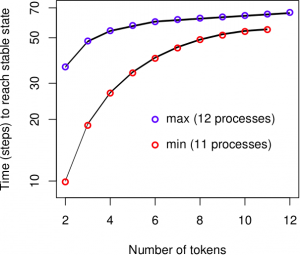
Then we study the average number of steps needed to reach the stable configuration according to the number of tokens initially present in the network. We compute the minimum and maximum expected rewards over all the schedulers. We plot the results obtained for two models with 11 an 12 processes. The blue and red dots are the results computed with PLASMA. The black lines are the exact values computed with PRISM. It shows that our results are within the 1% error bound specify by the Chernoff bound (with delta and epsilon equal to 0.01).