Description
A multi-lift system consists of a hierarchy of components, e.g., the system contains multiple lifts, floors, users, etc.; a lift contains a panel of buttons, a door and a lift controller; a lift controller may contain multiple control units. Ideally, the behavior system need to be formally verified to satisfy desirable properties. For instance, one of the properties is:
If a user has requested to travel in certain direction, a lift should not pass by (i.e., traveling in the same direction without letting the user in).
However, this property is not satisfied. Typically, once a user presses a button on the external panel at certain floor, the controller assigns the request to the “nearest” lift. If the nearest lift is not the first reaching the floor in the same traveling direction, the property is violated. One counterexample that could be returned by a standard model checker is that the lift is held by some user for a long time so that other lifts pass by the floor in the same direction
first. One solution is re-assign all external requests every time a lift travels to a different floor. Due to the complexity, many existing lift systems do not support re-assigning requests. The question is then:
What is the probability of violating the property, with typical randomized arrival of user requests from different floors or from the button panels inside the lifts?
An algorithm for assigning the requests can be chosen based on the value of this probability.
SystemC Model
The model consists two modules: liftsystem and user. At the beginning, every lifts are waiting for requests and at floor 0.
The module liftsystem contains N lifts and M floors. The liftsystem object has multiple data structures, e.g., a vector of integer for user requests from external button panels, a two dimension vector of integer for requests from internal button panels, a vector of lift_status_t data structure for the status of the lifts. For an external request from a certain floor, the controller will assign this request to the nearest lift (the distance is computed by the number of floors).
A lift is modeled as follows. If there is an external or internal request at the current floor, it serves and clears this request. Otherwise, it checks whether it should continue traveling in the same direction, or change direction, or simply idle. For each second, a lift can travel 1 floor.
The module user generates external and internal requests. There are (2M – 2 + NM) different requests for N lifts and M floors, in which (2M – 2) are external requests and NM are internal requests. We model the behavior of one user as follows:
Every second, a user generates a request. For simplicity, the probability that it is an external request from a particular floor for going up or going down is 2/N x 1/(2M-2), and the probability that it is an internal request for going to a particular floor is (N-2)/N x 1/NM.
We also define the variable passby (private attribute of the module liftsystem) which is true if and only if the lifts pass by. And the clock cycle of the SystemC simulation is set to be 1 second.
Instrumented Model for SMC
Assume that we want to use Plasma Lab to answer the question “what is the probability that the lifts pass by within 1000 seconds of simulation, with typical randomized arrival of user requests from different floors or from the button panels inside the lifts?“. In order to do that, first we need to instrument the SystemC model of the multi-lift system with MAG tool. MAG will generate the monitor and an aspect advice file used by AspectC++ to instrument automatically the SystemC model. In this example, we need to observe the value of the passby variable at the boundary of clock cycles (every second of simulation time), we declare the following triggers in the configuration file (for more details about MAG and configuration file): Important! Important!
where pnt_liftsystem is a pointer to liftsystem object. Then the following clock expression in the configuration file:
indicates that the generated monitor will sample the state of model (the value of passby) at boundary of clock cycle.
Important!
Our models can be downloaded here:- Plasma project: multi-lift_v1.tar.gz
- SystemC model (original and instrumented): multi-lift_v1_model.tar.gz
To execute the model user extracts and puts the plasma project directory into the same location of the Plasma Lab jar file. Then launch Plasma and open the Plasma project will need to open the Plasma project multilift_v1.plasma.
Verifying Property
After launch Plasma Lab and open the project, user can define any property in BLTL based on the primitives provided by the instrumented SystemC model as shown in the following figure
For example, to express the property “ the lifts pass by within 1000 seconds of simulation” with the above instrumented multi-lift system model in SystemC, user can write the following BLTL formula in Plasma Lab.
Important!
Experimental Results
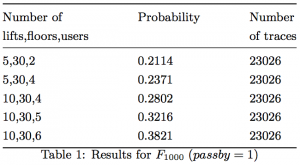
We applied the 2-sided Chernoff bound with the accuracy 0.01 and the level of confidence 1 – 0.02 = 0.98. Table 1 shows the probability of the property when changing different parameters of the model such as the numbers of lifts, floors, and users. We observe that the probability increases when the number of users increases. This means that with more requests per second, it is more likely that the lifts pass by. Similarly, the probability increases when the number of lifts increases. In the size of model, these results can be compared with those reported in numerical approaches, in which the state space explosion likely occurs when there are more than 3 lifts and 4 floors.
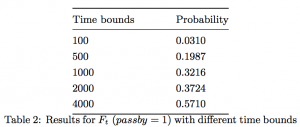
The second experiment, that changes the time bounds of model with 10 lifts, 30 floors, and 5 users, is reported in Table 2. Intuitively, when the model runs for a longer time, the probability that the lifts pass by increases as well.
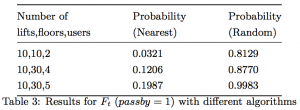
Lastly, we compare the algorithm assigning the nearest lift to a given request to an algorithm assigning a random one. Results are reported in Table 3. The time bounds are 100, 200, and 500 in the rows number 1, 2, and 3, respectively. The nearest assignment always performs better than the random assignment in all cases as we expect.