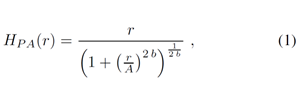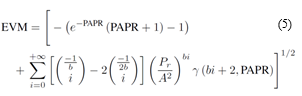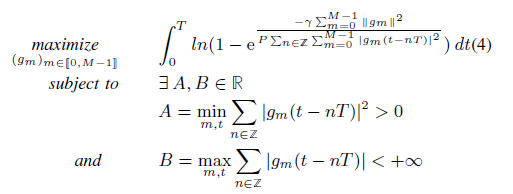PAPR reduction

• PhD Students: A. Cheaito, M. Chafii
• Partner involved: IETR SCEE, IRISA METISS, IETR SCN

Jump to

• Joint PAPR optimization and pre-distortion technics
• Study of a New Multi-Carrier Waveform

Jointed PAPR Optimization and Pre-Distortion technics

Current communication systems are requesting high connectivity, reliable transmission in mobility and increasing spectral efficiency. LTE, WiMAX, WiFi, DVB and other communication systems today use Orthogonal Frequency Division Multiplexing (OFDM) which is considered as one of the key technologies able to fulfill all these demands. However, OFDM has one major drawback which is the large fluctuations of the signal magnitude commonly characterized by the so-called Peak-to-Average Power Ratio (PAPR). Indeed, signals with a high PAPR value may experience strong distortions in and out of the band during the passage through nonlinear components such as the Power Amplifier (PA). In the literature, two main approaches are usually advocated to solve the problems of the PAPR and the non-linearity of the PA. The first one is to carry out PAPR reduction methods consisting in reducing the dynamics of the signal by means of dedicated signal processing. Among the large variety of PAPR reduction algorithms, the most popular are clipping, coding, Selected Mapping (SLM) and Tone Reservation (TR). The second approach which can be used in a complementary way with the former is to make use of linearization techniques that tries to compensate for the non-linearity of the PA. On this aspect, different solutions are possible such as Digital Pre- Distortion (DPD) , Linear Amplification with Non-linear Component (LINC) method and Feedback. Hence, an efficient implementation of a communication system in which the PAPR of the signals plays an important role should embed a PAPR reduction technique followed by a linearization process. Such implementation can for example be found in high or medium power transmits stations using OFDM at the physical layer, e.g. DVB-T2 towers or LTE nodes. Today however, all these treatments remain static and do not take into account transmission conditions. A smart solution for future implementations would be to control the PAPR reduction and linearization stages in a flexible way according to some predefined parameters so that they become adaptive and self-configurable. These parameters are metrics widely used to measure the performance of the linearization and the PAPR reduction. Noise Power Ratio (NPR), Adjacent Channel Power Ratio (ACPR) and Error Vector Magnitude (EVM) are examples of these parameters. In particular, EVM is a common figure of merit for assessing the quality of digital modulated telecommunication signals. Assuming a transmitter implementation with adaptive PAPR reduction and linearization processes, one can imagine controlling the DPD and the PAPR reduction stages to meet a various EVM target values related to different qualities of service. In that perspective, we are interested in the analytical derivation of the EVM of an OFDM signal after nonlinear amplification when DPD is used or not. Although some upper-bounds of the second order moment of the predistortion error and of the EVM can be found in the literature, to the best of our knowledge, no analytical expression exists in the literature. Our main contribution then consists in providing such a result as a function of the transition factor of the power amplifier characteristics and of the accuracy factor of the DPD function.

System description 

Fig.11 represents the block diagram of a simplified transmission chain equipped with a DPD stage receding the power amplifier. We denote x₁(t) the multicarrier signal generated by the system, x₂(t) the pre-distorted signal and z(t) the amplified output signal. As our contribution focuses on the impact of the predistortion in the computation of the EVM expression, no particular PAPR reduction process is considered here. The model of power amplifier used is the Rapp model given by (1), and predistortion function corresponding to Rapp model is given by (2).where a and b are the predistortion and PA knee factor respectively and A is the amplitude of the saturation output voltage of the amplifier.

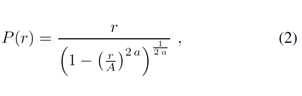 However, The EVM of the amplified signal Z_k is expressed as follows:

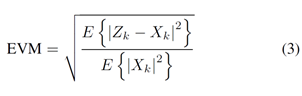
Where represents the second order moment of the error magnitude and E{|X_k|²} is the average signal power. Note that E{.}  is the expectation function.

Main results

After the theoretical calculation, we have these two EVM expressions without and with DPD given by (5) and (6) respectively:

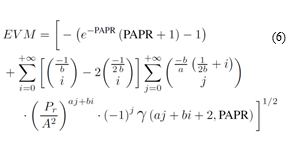Eventually, we obtain EVM expressions in the form of a series expansion involving Gamma functions and depending on the knee factor b, the predistortion knee factor b when the DPD is activated and the saturation power A² of the PA, as well as on the signal PAPR and the average power P_r. 

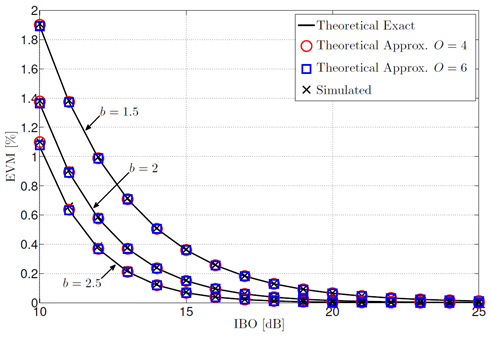
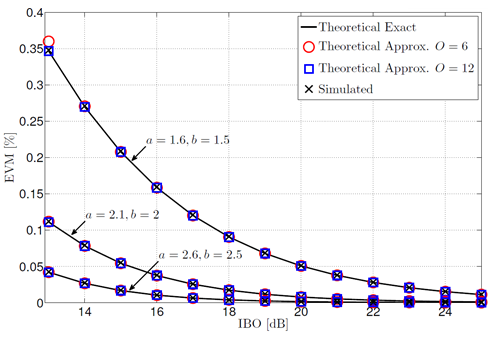
Fig. 12 depicts the theoretical (exact and approximated) and simulated EVM as a function of the IBO, without predistortion. In practice, note that the IBO commonly applied to the input signal is always more than 10dB to mitigate distortions. We consider knee factors b of 1:5; 2 and 2:5, and an OFDM signal with PAPR = 10dB. The approximated EVM results are given for O = 4 and O = 6. From the curves, we can observe that our proposed equation of the EVM matches exactly the exact and the simulated EVM for only O = 4 and O = 6. Fig. 13 shows the theoretical (exact and approximated) and simulated EVM when predistortion is used, with various couples of values for a and b, and with O = 6 and O = 12. Once again, our theoretical analyzes match perfectly the exact and simulated one proving the consistency of the proposed approximated EVM expressions.

This very recent work is a first step in the analytical study of a fully adaptive transmitter model, being able to be flexibly controlled according to the transmission conditions such as the input power, the amplifier and predistortion characteristics and the PAPR. This study is a part of the global optimization approach of the transmitter efficiency and linearity, which could be very useful for example to the current deployment of the DVB-T2 transmitters.

 

Study of a New-Multi-Carrier Waveform

Another way to reduce the fluctuations of the OFDM envelope is to act on the modulation scheme to construct a signal with low variations. The idea is to construct a new waveform that satisfies the constraint of a low PAPR. This idea is different from the other PAPR reduction techniques that are acting on the signal before and/or after the modulation while keeping the same modulation scheme.

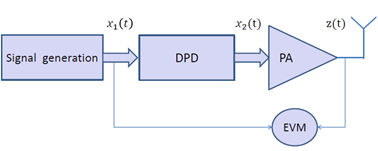
To start our investigation, we consider a generalized system that we name Generalized Waveforms for Multi-Carrier (GWMC) system, which is a modulation system based on any modulation scheme. We model the waveforms with a family of functions {g_m} _{m ∈ [0, M-1]}, the index m stands for the carrier index and M is the number of carrier. The objective is to find the optimal modulation functions that gives, at the output of the modulation, a multi-carrier signal with low PAPR.

In our investigation, we follow the following steps:

• We consider the following two constraints:
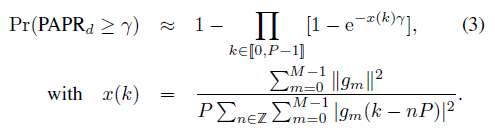
• Based on the previous PAPR expression, we model the PAPR reduction problem as a constrained optimization problem as expressed in Eq.(4). We optimize on the family of modulation functions {g_m} _{m ∈ [0, M-1]}, the PAPR performance under two constraints on the waveforms [3].

• In [4], we give a solution of the optimization problem. We conclude that, for all the modulation schemes that satisfy the previous constraints, the OFDM has an optimal PAPR performance. At the best of our knowledge, this is the first work that gives an analytical proof of the optimality of the OFDM in PAPR performance. In addition to that, the study identifies a large family of mutli-carrier systems which are optimum in terms of the PAPR performance, and thus have the same PAPR performance than the OFDM. It is true that we were hoping to find a new waveform better than OFDM as a solution of the optimization problem, but the result that we find is still important in the sense that he limited the optimality of the OFDM to the previous constraints and clarify why in the literature [5] [6], other MCM systems have the same or worse PAPR performance than OFDM. In addition to that, this result gives an idea about getting a better PAPR than OFDM, which is actually to release the first constraint.
• The OFDM is optimal in terms of PAPR performance, when the previous two constraints hold. But if the family {g_m} _{m ∈ [0, M-1]}, does not satisfy the first condition, it is possible to find a better PAPR performance than OFDM. That means that if there exists at least an index m₀ such that the waveform g_m0 has a temporal support less than the symbol period, and that means that its amplitude vanishes at least in time interval, then we can get a better PAPR performance than OFDM. The example in the literature is the Wavelet OFDM using the Inverse Discrete Wavelet Transform based on Haar wavelet for modulation, the PAPR is reduced by 2db [7]. The perspective of the work is to study the impact of releasing the first constraint on the system, and then acting on the temporal support of the function to construct a new waveform with low PAPR.

 

References

 

[5] A. Skrzypczak, P. Siohan, and J. P. Javaudin,”Peak-to-Average Power Ratio Issues for Pulse-Shaped Multicarrier Modulations,” in Advances on processing for multiple carrier schemes: OFDM and OFDMA, Faouzi Bader and Nizar Zorba,  pp. 43-90. Nova Science Publishers, Inc., 2011.

[6] A. Kliks, “New Transmission and Reception Techniques of the Generalized Multicarrier Signals, Ph.D. thesis, Poznan University of Technology, 2011.

[7] J. Zakaria, M. Salleh, “Wavelet-based OFDM Analysis: BER Performance and PAPR Profile for Various Wavelets”, IEEE Symposium on Industrial Electronics and Applications, September 2012, Bandung, Indonesia.