par Nicolas Schabanel, DR CNRS, LIAFA U. Paris Diderot – IXXI, ENS de Lyon
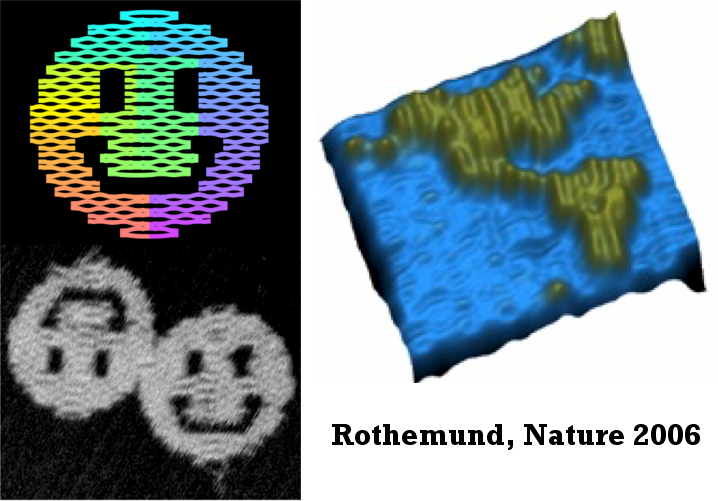
Ce cours sera une introduction à de nouveaux modèles de calcul qui sont effectivement implémentés en laboratoire dans des bechers par… des molécules. Ces calculs sont obtenus par exemple laissant des molécules à base d’ADN se replier sous forme de tuiles de taille nanoscopique, puis s’assembler par affinités pour réaliser des formes géométriques arbitraires de quelques centaines de nanomètres de diamètre. Le premier modèle effectif remonte à la thèse d’Erik Winfree en 1998 qui proposa le modèle d’auto-assemblage algorithme dont il démontra qu’il peut implémenter n’importe quel calcul Turing. Les premières étapes de son modèle furent ensuite réalisées en becher à l’aide de molécules d’ADN par Paul Rothemund qui obtint en 2001 une implémentation des triangles de Sierpinski. Depuis, différentes variantes ont été proposées aussi bien du côté des modèles théoriques, que des implémentations expérimentales. Ceux-ci ont permis la réalisation de smileys, cartes, alphabets, un compteur binaire (Evans, 2014)… nanoscopiques ainsi que tout récemment les prémices d’une robotique nanoscopique à base d’ADN, donc potentiellement compatible avec la vie. Ces modèles reposent sur un mélange, entre autres, de géométrie discrète, de calculabilité, d’automates cellulaires et d’algorithmique classique et randomisée. Dans ce cours, nous présenterons une introduction à ce nouveau type de calcul qui sera… qui sait… peut-être le futur post-silicone de nos ordinateurs !