- Title: “Time-dependent multimodal point to point shortest path”
- When: September 22, 2022 — 15:00
- Where: Amphithéâtre A1, Campus SophiaTech Lucioles, Sophia-Antipolis
- Committee:
- Mohammed Amine Ait Ouahmed (co-director), Research Engineer, Instant-System, Sophia Antipolis, France
- Leandro Calligari Coelho (referee), Professeur titulaire, Université Laval, Québec, Canada
- David Coudert (president), Senior Researcher (DR Inria), Inria, Sophia Antipolis, France
- Yann Hervouet (invited), CEO Instant-System, Sophia Antipolis, France
- Emmanuel Néron (referee), Professor, Université de Tours, France
- Jean-Charles Régin (co-director), Professor, I3S, Université Côte d’Azur, Sophia Antipolis, France
- Dorothea Wagner, Professor, Karlsruhe Institute of Technology, Germany
-
Abstract: Computing a route is a fundamental problem in our society. The shortest path problem has been studied for many years and is one of the best known problems in graph theory and operations research. A variant of this problem exists for public transit networks, with the need to modify the algorithms to take into account the temporality of public transit. Many algorithms exist, but new algorithms must be created to meet the needs of users. In this thesis, we study public transit routing and its use in mobility applications for smart phones. The first contribution is a multi-objective algorithm, to meet different user needs, which uses precomputation to decrease the response time. This algorithm is based on goal-directed search, so for a route between Nice and Cannes, the routes passing through Menton will not be studied.
The second contribution is the application of the k shortest path problem to public transit networks. The k shortest paths problem enumerates the shortest paths between a starting point and an ending point. Their application to public transit networks provides a large number of results with a very fast response time. Moreover, the results produced are often dissimilar, which allows to provide users with potentially interesting results.
The last contribution is an intermodal algorithm combining public transport and carpooling. Such an algorithm overcomes the disadvantages of each network: for public transit networks, the transit schedules may not satisfy the user’s needs, and for carpooling, finding a driver who passes by a user’s departure and arrival point is very rare. This algorithm responds to a frequent request from the modern world.
- Titre: “Recherche de plus court chemin multimodal de point à point dépendant du temps”
-
Résumé: Calculer un itinéraire est un problème fondamental dans notre société. Le problème du plus court chemin est étudié depuis de nombreuses années et fait partie des problèmes les plus connus en théorie des graphes et en recherche opérationnelle. Une variante de ce problème existe pour les réseaux de transports en commun, avec la nécessité de modifier les algorithmes pour prendre en compte la temporalité des transports en commun. De nombreux algorithmes existent, mais de nouveaux algorithmes doivent être créés pour répondre aux besoins des utilisateurs.
Dans cette thèse, nous étudions le calcul d’itinéraires pour les transports en commun et son utilisation dans des applications de mobilité pour smartphone. La première contribution est un algorithme multiobjectif, pour répondre aux différents besoins des utilisateurs, qui utilise du précalcul afin de diminuer le temps de réponse. Cet algorithme est basé sur la recherche guidée par le but, ainsi pour un itinéraire entre Nice et Cannes, les itinéraires passant par Menton ne seront pas étudiés.
La deuxième contribution est l’application du problème des k plus courts chemins aux réseaux de transports en commun. Le problème des k plus courts chemins énumère les plus courts chemins entre un point de départ et un point d’arrivée. Leurs applications aux réseaux de transports en commun permettent de fournir un grand nombre de résultats avec un temps de réponse très rapide. En outre, les résultats produits s’avèrent bien souvent dissimilaires, ce qui permet de fournir aux utilisateurs des résultats potentiellement intéressants.
La dernière contribution est un algorithme intermodal combinant les transports en commun et le covoiturage. Un tel algorithme permet de pallier les désavantages de chaque réseau : pour les réseaux de transports en commun, les horaires de passages peuvent ne pas satisfaire les besoins de l’utilisateur et pour le covoiturage, trouver un conducteur qui passe par le point de départ et d’arrivée d’un utilisateur est très rare. Cet algorithme répond à une demande fréquente des acteurs du monde moderne.
Author: dcoudert
New source code: Public Transit kSSP
We are pleased to announce the release of a collection of algorithms in Java for finding k earliest arrival time journeys in public transit networks.
- Source code: https://github.com/fink-arthur/PT-KSSP
- Authors: Ali Al Zoobi (Inria) and Arthur Finkelstein (Instant-System)
Best paper award at ICORES 2022
The paper On Finding k Earliest Arrival Time Journeys in Public Transit Networks, co-authored by Ali Al-Zoobi (Inria), David Coudert (Inria), Arthur Finkelstein (Instant-System) and Jean-Charles Régin (I3S), has received the best paper award of the 11th International Conference on Operations Research and Enterprise Systems (ICORES). The conference was online, February 3-5, 2022.
The code used to conduct experiments is here.
New source code: hyperbolicity
We are pleased to announce the release (version v2.0) of a collection of algorithms in C++ for computing the hyperbolicity of graphs. It includes algorithms enabling to compute the hyperbolicity of graphs with unprecedented size (up to a million nodes).
- Source code: https://gitlab.inria.fr/dcoudert/hyperbolicity/
- Authors: David Coudert, André Nusser and Laurent Viennot
PhD defense of Ali Al Zoobi
- Title: “Practical computation of simple paths with length and diversity constraints in complex and multimodal networks”
- When: November 25, 2021 — 10:30
- Where: Inria, Euler Violet and live on Youtube (https://youtu.be/M6ypcki8yF4)
- Committee:
- Mohammed Amine Ait Ouahmed, Research Engineer, Instant-System, Sophia Antipolis, France
- David Coudert (supervisor), Senior Researcher (DR Inria), Inria, Sophia Antipolis, France
- David Ilcinkas (referee), Senior Researcher (CR CNRS), LaBRI, Bordeaux, France
- Christian Laforest, Professor, ISIMA, LIMOS, Clermont-Ferrand, France
- Nicolas Nisse (supervisor), Senior researcher, Inria, Sophia Antipolis, France
- Jean-Charles Régin, Professor, I3S, Université Côte d’Azur, Sophia Antipolis, France
- Laurent Viennot (referee), Senior Researcher (DR Inria), IRIF, Paris, France
-
Abstract: The shortest path problem is one of the most studied problem in graph theory and operations research. A classic generalization of this problem is the problem of finding k shortest simple paths (kSSP for short). That is, the problem of finding a shortest, a second-shortest, etc. until a k-th shortest simple path from a source to a destination in a directed weighted graph. Yen (1971) proposed the state-of-the-art kSSP algorithm, with theoretical time complexity in [latex]O(kn(m+n\log{n}))[/latex], where n is the number of vertices and m is the number of arcs of the input digraph. Since then, the problem has been widely studied from an algorithmic engineering perspective, that is designing exact algorithms offering better performances in practice.
In this thesis, we study the kSSP problem from an algorithm engineering perspective. More precisely, we design new kSSP algorithms allowing to outperform the state-of-the-art algorithms in terms of running time, memory consumption, or offering a better space-time trade-off. We also show how to apply our algorithms in graphs with arbitrary arc weights without negative cycles.
Then, we study the problem of finding paths respecting dissimilarity constraints. Precisely, we study the complexity of the problem according to four different similarity measures, and we show in which cases the problem is NP-Complete or polynomial time solvable.
Finally, we show how to adapt the kSSP problem to a multimodal public transportation network model, i.e., combining metro, tram, buses, and walk. Precisely, we design some kSSP algorithms to solve a related problem, which is, the problem of finding k earliest arrival journeys from a source station to a destination station in a public multimodal transportation network. - Titre: “Calcul pratique de chemins simples avec des contraintes de longueur et de diversité dans des réseaux complexes et multimodaux”
-
Résumé: Le problème du plus court chemin est l’un des problèmes les plus étudiés en théorie des graphes et en recherche opérationnelle. Une généralisation classique de ce problème est le problème de trouver k plus courts chemins simples (kSSP). C’est-à-dire, le problème de trouver le plus court, le deuxième plus court, etc. jusqu’au k-ième plus court chemin simple d’une source à une destination dans un graphe orienté pondéré. Yen (1971) a proposé l’algorithme avec la meilleure complexité théorique connue pour résoudre le kSSP dans un graphe orienté pondéré à n sommets et m arcs, avec une complexité en [latex]O(kn(m+n\log{n}))[/latex]. Depuis, le problème a été largement étudié du point de vue de l’ingénierie algorithmique.
Dans cette thèse, nous étudions également le problème kSSP sous cet angle, c’est-à-dire que nous proposons des algorithmes exacts offrant de meilleures performances en pratique que l’état de l’art, en termes de temps d’exécution, de consommation mémoire ou offrant de meilleurs compromis espace-temps. Nous montrons aussi comment étendre nos algorithmes au cas des graphes avec des poids arbitraires sans cycles négatifs.
De plus, nous étudions le problème de trouver k plus courts chemins simples qui sont mutuellement dissimilaires. Plus précisément, nous étudions la complexité du problème en fonction de quatre mesures de similarité différentes, et nous montrons dans quels cas le problème est NP-Complet ou peut être résolu en temps polynomial.
Enfin, nous montrons comment adapter le problème kSSP à un modèle de réseau de transport public multimodal. Nous adaptons certains de nos algorithmes pour le kSSP au problème de trouver, dans un réseau de transport public multimodal, les k itinéraires d’une station source et à une station destination arrivant au plus tôt.
PhD defense of Nicolas Isoart
- Title: “The Traveling Salesman Problem in Constraint Programming”
- When: November 19, 2021 — 14:00
- Where: auditorium 0+229, Templiers site, Polytech Sophia Antipolis
- Committee:
- Reviewers
- Claude-Guy QUIMPER, Professeur, Université Laval
- Willem-Jan VAN HOEVE, Professeur, Carnegie Mellon University
- Xavier LORCA, Professeur, IMT Mines Albi-Carmaux
- Examiners
- Cambazard HADRIEN, Maître de conférences, Grenoble INP
- David COUDERT, Directeur de recherche, INRIA Sophia Antipolis
- Supervisor
- Jean-Charles RÉGIN, Professeur, Université Côte d’Azur
- Reviewers
-
Abstract: Several constraint programming (CP) models, based on Lagrangian relaxation (LR), have been introduced to solve the traveling salesman problem (TSP).
In this thesis, we define three new constraints and filtering algorithms based on the structure of the graph. First, the k-cutset constraint imposes that any solution contains a strictly positive and even number of elements in each cutset. Then, the mandatory Hamiltonian path constraint is based on the local search k-opt algorithm. If a path of mandatory edges is not optimal (i.e. it exists a k-opt), then it cannot belong to any optimal solution. Finally, the 1-tree constraint is based on the idea that if the problem can be decomposed in two independent sub-problems, then a part of the 1-tree can be optimal in a sub-problem.
In addition, to speed-up the practical performances, we introduce an algorithm named SSSA to avoid oscillations and non-variations of the objective function of LR, saving useless solving times.
We also parallelize the search for solutions with Embarrassingly Parallel Search (EPS). Unfortunately, a direct application of EPS does not lead to good results for the TSP. Indeed, the decomposition mechanism of EPS is a depth-bounded process whereas the search strategy used to solve the TSP is depth-first. Therefore, we define a diving algorithm fixing this issue. However, sub-problems with extremely different solving times may appear. Thus, we introduce a re-decomposition policy in EPS.
Finally, our experiments on the TSPLib showed that the structural constraints reduce the solving times by an order of magnitude. Moreover, we show that our version of EPS leads to a huge improvement related to the number of cores. - Titre: “Le problème du voyageur de commerce en programmation par contraintes”
-
Résumé: Plusieurs modèles de programmation par contraintes, basés sur la méthode de relaxation lagrangienne (LR), ont été introduits pour résoudre le problème du voyageur de commerce (TSP).
Dans cette thèse, nous définissons trois nouvelles contraintes et algorithmes de filtrage considérant la structure du graphe. La contrainte k-cutset impose que toute solution contienne un nombre strictement positif et pair d’éléments dans chaque cutset. La contrainte mandatory Hamiltonian path est basée sur l’algorithme de recherche locale k-opt. Si un chemin composé d’arêtes obligatoires n’est pas lui-même optimal (c.-à-d., il existe un k-opt), alors ce chemin n’appartient à aucune solution optimale. Enfin, la contrainte du 1-tree est basée sur l’idée que si le problème peut être décomposé en deux sous-problèmes indépendants, alors une partie du 1-tree peut être optimale dans un des sous-problèmes.
De plus, nous introduisons l’algorithme SSSA afin d’améliorer les temps de résolution. SSSA évite les oscillations et les non-variations de la fonction objective de la LR. Ensuite, nous parallélisons la recherche de solutions avec Embarrassingly Parallel Search (EPS). Malheureusement, le mécanisme de décomposition d’EPS est un processus à profondeur borné, contrairement à la stratégie de recherche utilisée pour résoudre la TSP qui est en profondeur d’abord. Cela rend difficile l’obtention de bons résultats en appliquant directement EPS. Afin de diminuer ce défaut, nous introduisons un algorithme de précalcul. Cependant, des sous-problèmes avec des temps de résolution extrêmement différents peuvent apparaître. Pour remédier à cela, nous introduisons une méthode procédant à des redécompositions dans EPS. Finalement, nous expérimentons sur la TSPLib. Nous montrons que les contraintes structurelles permettent de réduire les temps de résolution d’un ordre de grandeur, et que la parallélisation permet d’obtenir de très bons résultats liés au nombre de coeurs.
Presentation of Ali Al Zoobi at MT180 – UCA
Ali Al Zoobi presented his PhD topic at “ma thèse en 180 seconde” (MT180) – UCA. The presentation (in French), entitled “Trouver des chemins courts dans un réseau de transport”, is on YouTube.
New source code: k Shortest Simple Paths
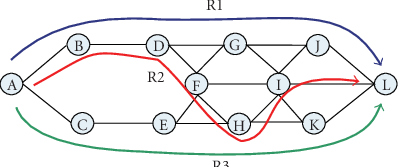
We are pleased to announce the release (version v1.0) of a collection of algorithms in C++ for solving the k shortest simple paths problem in weighted directed graphs.
- Source code: https://gitlab.inria.fr/dcoudert/k-shortest-simple-paths
- Authors: Ali Al Zoobi, David Coudert and Nicolas Nisse (INRIA Sophia Antipolis Méditerranée, COATI)
Presentation of Nicolas Isoart at MT180 – UCA
Nicolas Isoart presented his PhD topic at “ma thèse en 180 seconde” (MT180) – UCA. The presentation (in French), entitled “Recouvrement de graphes par des chemins sous contraintes”, is on YouTube.
New source code: Hub labeling based version of CSA and RAPTOR supporting unrestricted walking
We are pleased to announce the release of an implementation in C++ of HLCSA and HLRaptor which are variants of Connection Scan Algorithm (CSA) and RAPTOR supporting unrestricted walking through the use of a hub labeling of the footpath graph.
- Source code: https://github.com/lviennot/hl-csa-raptor
- Author: Laurent Viennot (INRIA Paris, GANG)


