Adaptive systems allow to model dynamic systems that adapt to their environment. They are composed by static programs and by transitions between these programs.These programs often have some common elements. Instead of keeping them separated they can be grouped, and their differences are model by sets of features. These features may be modified at runtime through a reconfiguration process.
The set of features of a system is organized in a feature model
is a set of system features
are the adaptive features (that can be reconfigured at runtime). The other features in
static.
are the environment features.
, where
and
is the powerset, is the set of valid configurations for all the features.
Feature expressions are used to identify sets of features that enable or disable some behaviors in the model.
Featured Timed Game Automata
In order to model adaptive systems with real time behaviors we have introduced in [CLST13] a model of Featured Timed Game Automaton. The model extends Timed Automata with features and introduces a notion of controllability that distinguishes the transition from the system from the ones of the environment. In PyECDAR Time Input/Output Automata are extended similarly with features. An example of FTGA is presented in the figure below, and further analysed with PyECDAR during the tutorial.
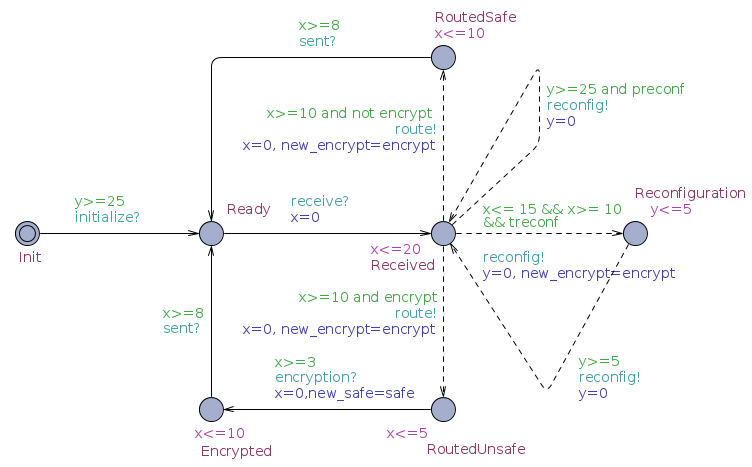 FTGA are provided with a game semantics similar to the one for TIOA. This allows to define strategies for the system and for the environment.
FTGA are provided with a game semantics similar to the one for TIOA. This allows to define strategies for the system and for the environment.
T-AdaCTL logic
Syntax
We have introduced in [CLST13] the T-AdaCTL logic to reason about reconfigurations in adaptive systems. This logic extends the AdaCTL logic from [CCHLS13] with timing constraints. The logic allows to reason about strategies, similarly to the ATL logic, with the game semantics of FTGA. Additionally it includes an operator to reason about features. The logic has three levels of formulae:
- Feature formula have the form
, where
is a feature expression and
is a state formula.
- State formula have the form
where a is a proposition,
are feature formulae, and
is a path formula.
- Path formula are classical from the TCTL logic. They have the form:
where
are feature formulae, I is an interval with integral bounds. U is called the until operator and W is called the weak until operator.
The grammar of the T-AdaCTL logic used by PyECDAR can be found on the queries section.
Semantics
A state in FTGA is composed by a location, a valuation of the real-time clocks, and a feature configuration. Informally the semantics of the logic is the following (formal definitions can be found in [CLST13]):
- A state satisfies a feature formula
, if either its feature configuration does not satisfy the feature expression
, or the state satisfies
- A state satisfies a state formula
if there exists a strategy for the system such that the path formula
is satisfied, whatever is the strategy of the environment.
- A state satisfies a state formula
if there exists a strategy for the system and a strategy for the environment (therefore they cooperate) such that the path formula
is satisfied.
The semantics of path formulae and the other state formulae are classical from CTL and TCTL.
Model-checking
We propose in [CLST13] model-checking algorithms to check T-AdaCTL formulae. These algorithms applies a classical backward propagation used for timed games algorithms. They are implemented in PyECDAR.

