Robustness

The final goal to in model based design is to implement in the end a software that will run on physical hardware. Eventually, at some stage in the design, it will be necessary to confront the abstract models, whose real time clocks are infinitely precise, to imprecise hardware clocks. This problem of the implementability of abstract models can be solved by checking the robustness of the models, that is to say their ability to accept some perturbations without deviating from the top level specifications. In [LLTW11] we have studied the robustness of timed specifications defined previously.

Perturbation of implementations and robust satisfaction

We apply a perturbation on the implementation components for a value . On physical systems the output urgent condition of implementations cannot be enforced and output actions will tend to happen either a bit earlier or a bit later. To model this behavior we extend the guards of output transitions and the invariants of the TIOA. For instance:

• a guard  becomes
• a guard  becomes

Conversely, receiving inputs at the limit of timing constraint may lead to chaotic behaviors. We model this by restricting the guards of input transitions, and the behaviors removed will be replaced by universal state (where any action may happen at any time) to model unpredictability. Then:

• a guard  becomes
• a guard  becomes

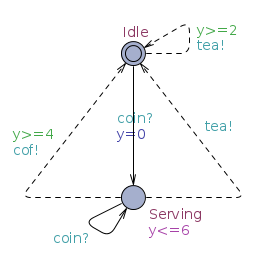
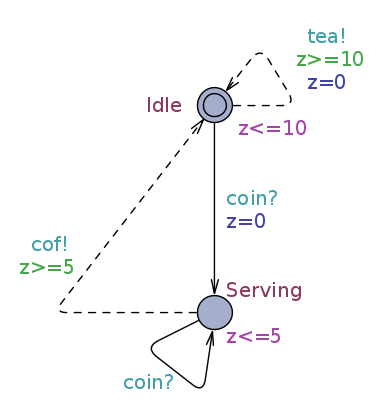
Specification	Implementation:	Perturbation of the implementation:

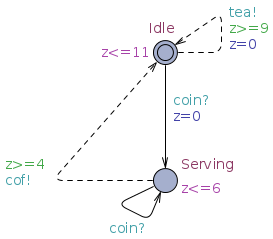
Robust satisfaction: An implementation of a specification is robust for a value if and only if its perturbation by refines the specification. In the example above we can check that: . We show that robust satisfaction is monotonic for different value of :

Robust games

In the problem of robust consistency we want to determine if a specification admits a robust implementation for a given perturbation. In the non-robust case, consistency is solved through a timed games. Therefore we have adapted the technique from [CHP08] to solve robust timed games. The technique consists in applying a transformation that allows to solve a robust game with classical timed games algorithms. In [LLTW11] we have adapted  this technique to timed specifications. The principle of this transformation is illustrated in the figure below. From the original game automaton A, we encode the perturbation by modifying the moves of the output player. Then, we show that solving a classical timed game on the robust automaton allows to solve a robust game on the original game automaton.

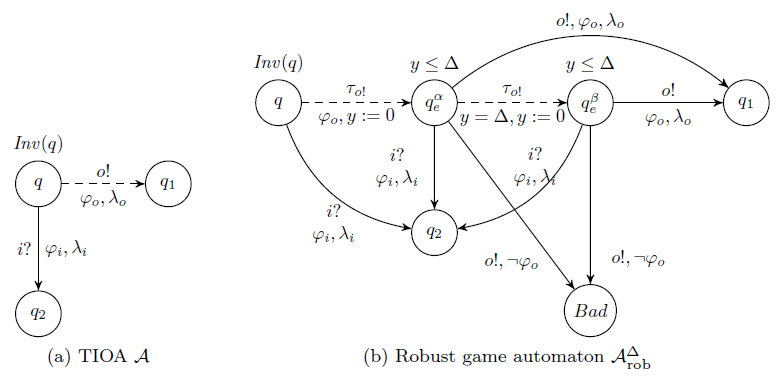This technique is also used to solve robust compatibility, i.e to determine if there exists an environment that is compatible with two specifications, even if it is subjected to some perturbation.

We show that the operators of the timed specifications theories (conjunction, parallel composition and quotient), remain are robust, i.e. their properties remains valid with respect to robust implementations. In particular the independent implementation property for parallel composition is also valid for robust implementations:

Parametric robustness problems

More than checking robustness for a given value of the perturbation, the designer of a system wants to know what is the maximum perturbation allowed by its models. This implies to solve parametric version of the previous problems robust satisfaction, robust consistency and robust compatibility) where the value of is unknown.

We have proposed in [Tra12] a counter-example technique (CEGAR approach) to evaluate this maximum value. The technique consists in solving a game for a given value of and refining the results (the counter-example strategy computed) by a parametric analysis to quickly converge to the solution.

Using this technique implemented in PyECDAR we can computes that the specification is robustly consistent for any value of lower than 3.