Timed specifications are an extension of timed automata (TA) models that are classically used to model timed systems. This complete specification theory allows to reason about specifications, models for requirements, and their implementations, whose timing behaviors are deterministic, through a satisfaction relation, a refinement relation and a set of operators to combine specifications (parallel composition, conjunction, quotient). This theory is explained in details in [DLLNW10]. We give below a short introduction to the theory.
The theory is build upon timed Input/Output automata (TIOA) that are TA whose alphabet is split between output actions, that represent the system, and input actions, that represent its environment. The two basic components of the theory are:
- Specifications: TIOAs that are input-enabled (input actions may be received in any state) and action deterministic (the same action always lead to the same state). See the example below.
- Implementations: specifications that additionally are output urgent (an output action cannot be delayed), and satisfy an independent progress condition (there is no time locks, even when no input is received). See the example below.
 |
 |
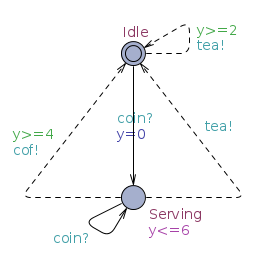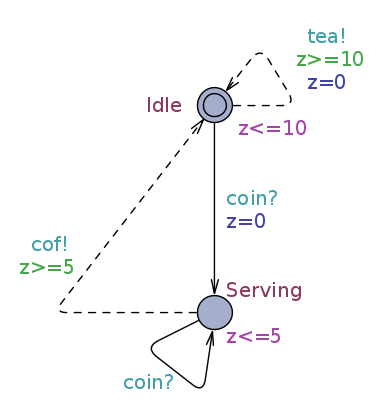Specification  |
Implementation  |
Whereas time automata theory uses real time logic formulae to express requirements, and checks whether a TA satisfies a given formula, specification theories use a refinement relation (denoted by ≤) to compare specifications and a satisfaction relation to check whether an implementation satisfies a specification. In timed specifications both refinement and satisfaction are defined with an alternating timed simulation.
For example the implementation above satisfies the specification:
Complex systems can be designed by combining several specifications with a set of operators:
- The conjunction of two specifications computes a specification that represent the intersection of their set of implementations.
- Parallel composition allows to combine two components that can communicate by synchronizing input and output actions. Refinement is a pre-congruence with respect to parallel composition:
This property allows to implements independently two specifications and then composed their implementations. - Quotient is a dual to parallel composition that allows to compute a difference between two specifications. We have that for any implementation X:
Specifications are equipped with a game semantics between two players: output, that plays with output actions, and input, that plays with input actions. Then a TIOA defines a concurrent game using a semantics similar to the one used in the tool Uppaal-Tiga.
A specification is consistent if and only if there exists an implementation that satisfies it. This can be checked using a timed game in which the output player tries to synthesize an implementation, while the input tries to prevent it by reaching a deadlock (inconsistent) state.
The theory also defines a notion of compatibility between two components to determine if they can be composed together in a useful environment. This can also be checked with a timed game, in which the input player now tries to synthesize a compatible environment, while output tries to prevent it by reaching an incompatible state.
