General description
The ActiveSet class provides a solver of quadratic programming problem using an active set method.
Definition
Quadratic programming (QP) is a type of optimization problem. It is the problem of optimizing (minimizing or maximizing) a quadratic function of several variables subject to linear constraints. The quadratic programming problem can be formulated as follows :
Suppose  is a positive integer representing the number of variables and
is a positive integer representing the number of variables and 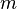 is a positive integer representing the number of constraints. Suppose
is a positive integer representing the number of constraints. Suppose 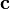 is a
is a  -dimensional real vector,
-dimensional real vector,  is a
is a 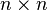 real symmetric matrix,
real symmetric matrix,  is a
is a 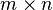 real matrix, and
real matrix, and  is a
is a 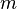 -dimensional real vector.
-dimensional real vector.
The quadratic programming problem is :
| minimize |  |
| subject to | 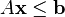 |
The notation 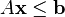 means that every entry of the vector
means that every entry of the vector  is less than or equal to the corresponding entry of the vector
is less than or equal to the corresponding entry of the vector 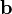 .
.
Algorithm
The process involves two phases:
1 – Feasibility phase: Find a feasible point, i.e a point that satisfies the constraint Ax≤b, while the objective is ignored. To find that point, we use the first step of the simplex method.
2 – Optimality phase: The objective is minimized while feasibility is maintained. It involves the generation of an iterative sequence of feasible points that converges to the solution.
In the following, we will suppose that Q is a symmetric positive-definite matrix. Note that there is no loss of generality in assuming that Q is a symmetric matrix, because if not, replacing Q by (Q+QT)/2 (which is symmetric) leaves the problem unchanged. Let’s describe step by step the method :
A – Quadratic program with linear equality constraint
Let consider the following quadratic program:
minimize 1/2 xTQx + cTx
subject to Ax = b
Using Lagrange’s method (KKT conditions), solving this program is equivalent to solving the system:
QxT + ATλ + c = 0
Ax = b
with λ a slack variable. This linear problem can be solved easily using for example a conjugate gradient algorithm.
B – Quadratic program with inequality constraint
Given an initial feasible point x0 and an initial working set W0 (indices of active constraints), the method relies on finding a descent direction dk so that the next iteration xk+1=xk+dk converges to the solution. To find such a dk, we solve the following sub-problem:
minimize 1/2(xk+ dk)TQ(xk+ dk) + cT(xk+ dk)
subject to AWk(xk+ dk)=b
with AWk the matrix of ai , the rows of A, with i in the working set. As xk is known at this step, this sub problem remains as a quadratic program whit linear equality constraint.
C – Descent direction process
If dk = 0, xk is an optimal solution with respect to the working set Wk. We compute the corresponding Lagrange multipliers λ. If λi = min(λj) < 0, it indicates that the objective function can be further optimized by making the corresponding constraints i inactive. Otherwise, the solution is optimal for the QP problem.
If dk ≠ 0, we find the step αk such that xk+1=xk+αk*dk activates the nearest next constraint:
αk = min( (bi – aiT*xk) / aiT*dk , 1. )
If αk < 1, we add the indice i, corresponding to the value taken for αk, to the set of active constraints.
D – Find a feasible solution
x0 = 0 is often a feasible solution. When it’s not, we can find a feasible solution by performing the first phase of the simplex method.




